
【题目】勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股数组可以发现,4=1×(3+1),12=2×(5+1),24=3×(7+1),…分析上面规律,第5个勾股数组为_____.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 ![]() .
. 
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数yl=x(x≥0), ![]() (x>0)的图象如图所示,则结论: ①两函数图象的交点A的坐标为(3,3);
(x>0)的图象如图所示,则结论: ①两函数图象的交点A的坐标为(3,3);
②当x>3时,y2>y1;
③当x=1时,BC=8;
④当x逐渐增大时,yl随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,若“摸出的球是黑球”为必然事件,求m的值;
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF= . 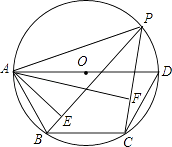
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.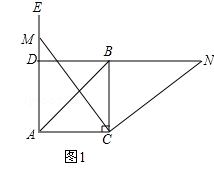
(1)直接写出∠NDE的度数.
(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由.

(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=![]() ,其他条件不变,求线段AM的长.
,其他条件不变,求线段AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com