
(10分)
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
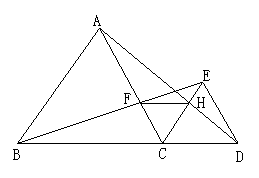
(1)求证:△BCE≌△ACD;
(2)求证:FH‖BD.
证明略
解析:(1)证明:∵△ABC和△CDE都是等边三角形
∴BC=AC,CE=CD,∠BCA=∠ECD=60°
∴∠BCA+∠ACE=∠ECD+∠ACE即∠BCE=∠ACD
∴在△BCE和△ACD中, 
∴△BCE≌△ACD (SAS).
(2)证法一:由(1)知△BCE≌△ACD,∴∠CBF=∠CAH,BC=AC
又∵△ABC和△CDE都是等边三角形,且点B、C、D在同一条直线上
∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF
∴在△BCF和△ACH中, 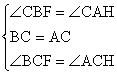
∴△BCF≌△ACH (ASA)
∴CF=CH又∵∠FCH=60°∴△CHF为等边三角形
∴∠FHC=∠HCD=60°∴FH‖BD
(证法二,本题也可由△CFE≌△CHD(ASA)得出△CHF为等边三角形)


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
(本题满分10分)如图,已知![]() ,以
,以![]() 为直径,
为直径,![]() 为圆心的半圆交
为圆心的半圆交![]() 于点
于点![]() ,点
,点![]() 为弧CF的中点,连接
为弧CF的中点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 为△ABC的角平分线,且
为△ABC的角平分线,且![]() ,垂足为点
,垂足为点![]() .
.
(1)求证:![]() 是半圆
是半圆![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分10分)
如图,已知OA⊥OB,OA=8,OB=6,以AB为边作矩形ABCD,使AD=a,过点D作DE垂直OA的延长线交于点E.
(1)求证:△OAB∽△EDA;
(2)当a为何值时,△OAB与△EDA全等?并求出此时点C到OE的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012届浙江省杭州市九年级第一次中考模拟考试数学卷 题型:选择题
(本题满分10分)如图,已知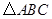 ,以
,以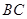 为直径,
为直径,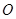 为圆心的半圆交
为圆心的半圆交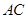 于点
于点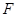 ,点
,点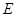 为弧CF的中点,连接
为弧CF的中点,连接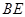 交
交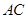 于点
于点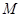 ,
,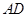 为△ABC的角平分线,且
为△ABC的角平分线,且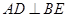 ,垂足为点
,垂足为点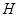 . [来源:]
. [来源:]
(1)求证: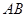 是半圆
是半圆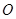 的切线;
的切线;
(2)若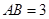 ,
,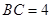 ,求
,求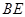 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东聊城卷)数学 题型:解答题
(11·柳州)(本题满分10分)
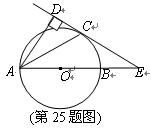
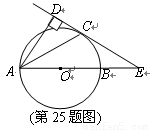
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=时,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com