
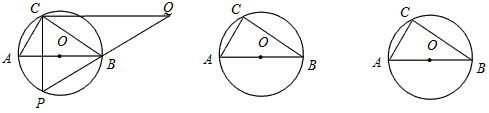
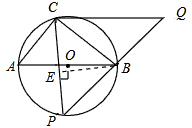
| 解:(1)∵AB为⊙O的直径, ∴∠ACB =90°, 在Rt△PCQ中,∠PCQ=∠ACB=90°, ∵∠CPQ=∠CAB, ∴△ABC∽△PQC; (2)当点P运动到与点C关于AB对称时,此时CP⊥直径AB于D, ∴CP=2CD, ∵AB=10, BC∶CA=4∶3, ∴BC=8,AC=6, 又∵AC·BC=AB·CD, ∴CD=4.8, ∴CP=2CD=9.6, ∵△ABC∽△PQC, ∴ 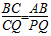 , ,∴CQ=12.8, (3)因为点P在⊙O上运动过程中,始终有△ABC∽△PQC, 所以PC最大时,CQ取到最大值, ∴当PC过圆心O,即PC 取最大值10时,CQ最大,最大为 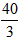 ; ;(4)当点P运动到弧CP的中点时,如图所示,过点B作BE⊥PC于点E, ∵P是弧AB的中点,∠PCB=45°, ∴∠PCA=45°,在Rt△CBE中, ∴CE=BE=4 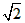 , ,易证:△ABC∽△PBE, ∴PE=3 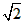 , ,∴CP=7 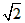 , ,∴CQ=7 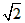 × ×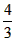 = =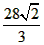 。 。 |
 |


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
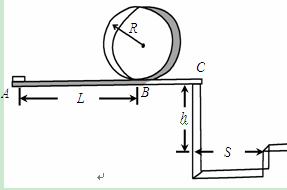
查看答案和解析>>
科目:初中数学 来源: 题型:
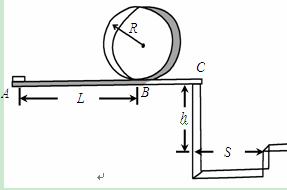
查看答案和解析>>
科目:初中数学 来源: 题型:
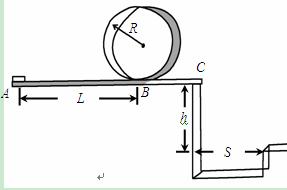
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com