
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ��ٷ�չ��С���ƻ������ѿ��һ������Ʒ�����˽��мס������ҿ�ݹ�˾�ȽϺ��ʣ���˾��ʾ�������Ʒ������1ǧ�˵ģ���ÿǧ��22Ԫ�շѣ�����1ǧ�ˣ������IJ��ְ�ÿǧ��15Ԫ�շѣ��ҹ�˾��ʾ����ÿǧ��16Ԫ�շѣ����Ӱ�װ��3Ԫ����С�������Ʒxǧ����
��1����ֱ�д���ס������ҿ�ݹ�˾��ݸ���Ʒ�ķ���y��Ԫ����x��ǧ�ˣ�֮��ĺ�����ϵʽ��
��2��С��ѡ���ļҿ�ݹ�˾��ʡǮ��
���𰸡���1��![]() ��
��![]() ����2����
����2����![]() ��x��4ʱ��ѡ�ҿ�ݹ�˾ʡǮ����x=4��x=
��x��4ʱ��ѡ�ҿ�ݹ�˾ʡǮ����x=4��x=![]() ʱ��ѡ�ס������ҿ�ݹ�˾��ݷ�һ���ࣻ��0��x��
ʱ��ѡ�ס������ҿ�ݹ�˾��ݷ�һ���ࣻ��0��x��![]() ��x��4ʱ��ѡ��ݹ�˾ʡǮ��
��x��4ʱ��ѡ��ݹ�˾ʡǮ��
��������
�����������1�����ݡ���˾�ķ���=��+�������������ص��ۡ��ɵó�y������x�ĺ�����ϵʽ�����ݡ��ҹ�˾�ķ���=�������������+��װ���á����ɵó�y������x�ĺ�����ϵʽ��
��2����0��x��1��x��1����������ۣ��ֱ���y����y����y��=y����y����y���������x�ķ��̻�ʽ���ɵó����ۣ�
�����������1��������֪��
��0��x��1ʱ��y��=22x����1��xʱ��y��=22+15��x��1��=15x+7��y��=16x+3��
��![]() ��
��![]() ��
��
��2���ٵ�0��x��1ʱ����y����y������22x��16x+3����ã�0��x��![]() ��
��
��y��=y������22x=16x+3����ã�x=![]() ��
��
��y����y������22x��16x+3����ã�![]() ��x��1��
��x��1��
��x��1ʱ����y����y������15x+7��16x+3����ã�x��4��
��y��=y������15x+7=16x+3����ã�x=4��
��y����y������15x+7��16x+3����ã�0��x��4��
���Ͽ�֪����![]() ��x��4ʱ��ѡ�ҿ�ݹ�˾ʡǮ����x=4��x=
��x��4ʱ��ѡ�ҿ�ݹ�˾ʡǮ����x=4��x=![]() ʱ��ѡ�ס������ҿ�ݹ�˾��ݷ�һ���ࣻ��0��x��
ʱ��ѡ�ס������ҿ�ݹ�˾��ݷ�һ���ࣻ��0��x��![]() ��x��4ʱ��ѡ��ݹ�˾ʡǮ��
��x��4ʱ��ѡ��ݹ�˾ʡǮ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A����3����2������ƽ��2����λ��������ƽ��2����λ����B�����B������Ϊ��������
A.��1��0��
B.��1����4��
C.����1��0��
D.����5����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
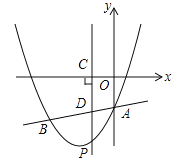
����Ŀ����ͼ��������![]() ��ֱ��
��ֱ��![]() ����A��B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��
����A��B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��
��1���������ߵĽ���ʽ��
��2����O��A��P��DΪ�����ƽ���ı����Ƿ���ڣ�����ڣ����P�����ꣻ�������ڣ�˵��������
��3������P�˶���ֱ��AB�·�ijһ��ʱ������P��PM��AB������ΪM������PAʹ��PAMΪ����ֱ�������Σ���ֱ��д����ʱ��P��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y����x��1��2�����н�����ȷ���ǣ�������
A. ��x��0ʱ��y��x���������СB. ��x��0ʱ��y��x�����������
C. ��x��1ʱ��y��x���������СD. ��x����1ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ2x3��5x2+x��1�����ʽ3x3+��2m��1��x2��5x+3�ĺͲ����������m=��������
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ��� y=��x-1��2+2 ��ͼ��������˵����ȷ���ǣ� ��
A. �������� B. ���������ǣ�1��2�� C. �Գ����� x=-1 D. �����ֵ�� 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
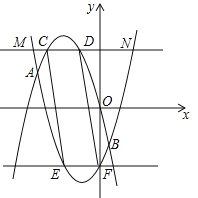
����Ŀ����ͼ����֪���κ���![]() ������2��4��������4��4��������
������2��4��������4��4��������
��1������κ���![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ��x�ᷭ�ۣ�������ƽ��2����λ���õ�������
��x�ᷭ�ۣ�������ƽ��2����λ���õ�������![]() ��ֱ��y=m��m��0����
��ֱ��y=m��m��0����![]() ��M��N���㣬���߶�MN�ij��ȣ��ú�m�Ĵ���ʽ��ʾ����
��M��N���㣬���߶�MN�ij��ȣ��ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2���������£�![]() ��
��![]() ����A��B���㣬���ֱ��y=m��
����A��B���㣬���ֱ��y=m��![]() ��
��![]() ��ͼ���γɵķ�����߽���C��D���㣨C����ࣩ��ֱ��y=��m��
��ͼ���γɵķ�����߽���C��D���㣨C����ࣩ��ֱ��y=��m��![]() ��
��![]() ��ͼ���γɵķ�����߽���E��F���㣨E����ࣩ����֤���ı���CEFD��ƽ���ı�����
��ͼ���γɵķ�����߽���E��F���㣨E����ࣩ����֤���ı���CEFD��ƽ���ı�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
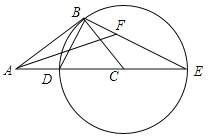
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣬��CBΪ�뾶����C����AC�ڵ�D����AC���ӳ����ڵ�E������ED��BE��
��1����֤����ABD�ס�AEB��
��2����![]() ʱ����tanE��
ʱ����tanE��
��3���ڣ�2���������£�����BAC��ƽ���ߣ���BE���ڵ�F����AF=2�����C�İ뾶��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com