
 在Rt△ABC中,∠ACB=90°,AB=5,
在Rt△ABC中,∠ACB=90°,AB=5, ,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE交直线BC于点F.
,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE交直线BC于点F. 时,求线段BF的长;
时,求线段BF的长; 时,求线段AD的长.
时,求线段AD的长. ,
,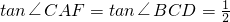 ,
, ,BF=
,BF=
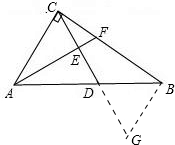
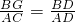 ,即
,即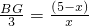 ①
①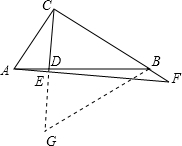
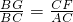 ,即
,即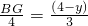 ,②
,②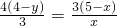 ,
,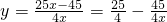
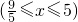
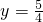 代入
代入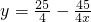 解得
解得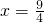 ,
,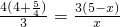 ,解得
,解得
 时,线段AD的长为
时,线段AD的长为 或
或
 ,可知
,可知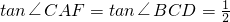 ,求得CF,从而求得线段BF的长;
,求得CF,从而求得线段BF的长;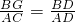 ,再由(1)得
,再由(1)得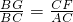 ,根据以上两个式子求出y关于x的函数解析式,
,根据以上两个式子求出y关于x的函数解析式, 或
或 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com