
分析 先利用待定系数法求抛物线的解析式,表示其顶点坐标和对称轴,再求直线AC的解析式,求M的坐标,知道AN=ND=1=MN,得△AMN、△AND、△AOC都是等腰直角三角形,则∠NAD=∠NDA=45°=∠CAB=∠AMN,设P(2,y),
分两种情况:当P在D的下方和上方时,证明△CMP∽△ADP和△CPA∽△CPM,列比例式可求出y的值,写出点P的坐标.
解答 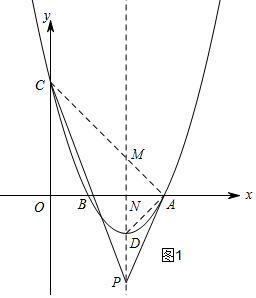 解:设抛物线的解析式为:y=ax2+bx+c,
解:设抛物线的解析式为:y=ax2+bx+c,
把A(3,0)、B(1,0)、C(0,3)代入得:$\left\{\begin{array}{l}{9a+3b+c=0}\\{a+b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为:y=x2-4x+3=(x-2)2-1,
顶点为D(2,-1),对称轴为:直线x=2,
设对称轴与x轴的交点为N,连接AC、AD,
设直线AC的解析式为:y=kx+b,
把A(3,0)、C(0,3)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线AC的解析式为:y=-x+3,
当x=2时,y=-2+3=1,
∴对称轴与直线AC的交点M(2,1),
∴AN=ND=1=MN,
∴根据勾股定理得:MC=2$\sqrt{2}$,AD=$\sqrt{2}$,∠NAD=∠NDA=45°=∠CAB=∠AMN,
分两种情况:
①当P在D的下方,如图1,设P(2,y),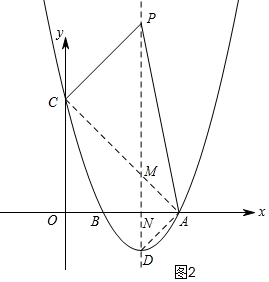
∵∠APC=45°,
∴∠CPD+∠APD=45°,且∠DAP+∠APD=45°,
∴∠CPD=∠DAP,且∠CMN=∠PDA=135°,
∴△CMP∽△ADP,
∴$\frac{CM}{DP}=\frac{PM}{AD}$,
∴$\frac{2\sqrt{2}}{-1-y}=\frac{1-y}{\sqrt{2}}$,
∴y=-$\sqrt{5}$,
∴P(2,-$\sqrt{5}$),
②当P在D的上方时,如图2,同理可证△CPA∽△CPM,
∴$\frac{AC}{PC}=\frac{PC}{MC}$,
∴PC2=AC•MC,
∴22+(y-3)2=3$\sqrt{2}$•$\sqrt{{2}^{2}+{2}^{2}}$,
(y-3)2=8,
y=3±2$\sqrt{2}$,
∵y>0,
∴y=3+2$\sqrt{2}$,
∴P(2,3+2$\sqrt{2}$),
综上所述,点P的坐标为(2,-$\sqrt{5}$)或(2,3+2$\sqrt{2}$).
点评 本题考查了二次函数的性质及图象上的点的坐标特点,先设所求点的坐标,并根据函数的关系式求出相关的点的坐标及线段的长,本题找到一对相似三角形列比例式是关键,与方程结合求出点P的坐标.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 零是绝对值最小的数 | B. | 倒数等于本身的数只有1 | ||
| C. | 相反数等于本身的数只有0 | D. | 原点左边的数离原点越远就越小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 精确到亿位 | B. | 精确到百分位 | C. | 精确到百万位 | D. | 精确到千万位 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )
如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )| A. | AD=BD | B. | AC=OC | C. | ∠CAD=∠CBD | D. | ∠OCA=∠OCB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com