
 由于矩形和菱形特殊的对称美和矩形的四个角都是直角,从而为密铺提供了方便,因此墙砖一般设计为矩形,而且图案以菱形居多,如图3所示,是长为30cm,宽为20cm的一块矩形瓷砖,E、F、G、H分别是矩形四边的中点,阴影部分为黄色,其它部分为淡蓝色,现有一面长为6m,高为3m的墙面准备贴这种瓷砖,那么:这面墙要贴的瓷砖数及全部贴满后这面墙上最多出现的与图3中面积相等的菱形个数分别为
由于矩形和菱形特殊的对称美和矩形的四个角都是直角,从而为密铺提供了方便,因此墙砖一般设计为矩形,而且图案以菱形居多,如图3所示,是长为30cm,宽为20cm的一块矩形瓷砖,E、F、G、H分别是矩形四边的中点,阴影部分为黄色,其它部分为淡蓝色,现有一面长为6m,高为3m的墙面准备贴这种瓷砖,那么:这面墙要贴的瓷砖数及全部贴满后这面墙上最多出现的与图3中面积相等的菱形个数分别为
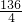 =34块淡蓝色菱形,
=34块淡蓝色菱形,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com