
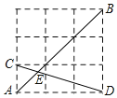
【题目】如图,在由边长为1的小正方形组成的网格中.点 A,B,C,D 都在这些小正方形的格点上,AB、CD 相交于点E,则sin∠AEC的值为_____.
科目:初中数学 来源: 题型:
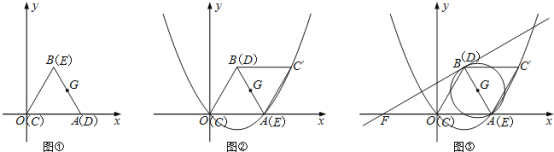
【题目】如图①②,在平面直角坐标系中,边长为2的等边![]() 恰好与坐标系中的
恰好与坐标系中的![]() 重合,现将
重合,现将![]() 绕边
绕边![]() 的中点
的中点![]() 点也是
点也是![]() 的中点),按顺时针方向旋转
的中点),按顺时针方向旋转![]() 到△
到△![]() 的位置.
的位置.
(1)求![]() 点的坐标;
点的坐标;
(2)求经过三点![]() 、
、![]() 、
、![]() 的抛物线的解析式;
的抛物线的解析式;
(3)如图③,![]() 是以
是以![]() 为直径的圆,过
为直径的圆,过![]() 点作
点作![]() 的切线与
的切线与![]() 轴相交于点
轴相交于点![]() ,求切线
,求切线![]() 的解析式;
的解析式;
(4)抛物线上是否存在一点![]() ,使得
,使得![]() .若存在,请求出点
.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
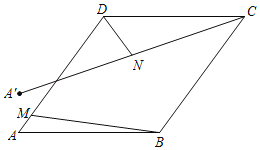
【题目】如图,菱形ABCD的边长为10,sinA=![]() ,点M为边AD上的一个动点且不与点A和点D重合,点A关于直线BM的对称点为点A',点N为线段CA'的中点,连接DN,则线段DN长度的最小值是_____.
,点M为边AD上的一个动点且不与点A和点D重合,点A关于直线BM的对称点为点A',点N为线段CA'的中点,连接DN,则线段DN长度的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为80元,用180元购进甲种玩具的件数与用300元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共32件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1350元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户,一次性收购了![]()
![]() 小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养![]() 天的总成本为
天的总成本为![]() 万元;放养
万元;放养![]() 天的总成本为
天的总成本为![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是![]() 万元,收购成本为
万元,收购成本为![]() 万元,求
万元,求![]() 和
和![]() 的值;
的值;
(2)设这批小龙虾放养![]() 天后的质量为
天后的质量为![]() (
(![]() ),销售单价为
),销售单价为![]() 元/
元/![]() .根据以往经验可知:m与t的函数关系式为
.根据以往经验可知:m与t的函数关系式为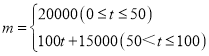 ,y与t的函数关系如图所示
,y与t的函数关系如图所示
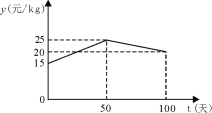
①求y与t的函数关系式;
②设将这批小龙虾放养t天后一次性出售所得利润为W元,求当![]() 为何值时,W最大?并求出W的最大值.(利润=销售总额-总成本)
为何值时,W最大?并求出W的最大值.(利润=销售总额-总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是( )
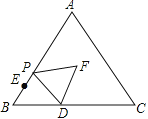
A. 8 B. 10 C. 3π D. 5π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:
类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.

理解应用:
(1)请仿照上面的竖式方法计算:![]() ;
;
(2)已知两个多项式的和为![]() ,其中一个多项式为
,其中一个多项式为![]() .请用竖式的方法求出另一个多项式.
.请用竖式的方法求出另一个多项式.
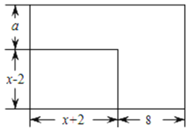
(3)已知一个长为![]() ,宽为
,宽为![]() 的矩形
的矩形![]() ,将它的长增加8.宽增加
,将它的长增加8.宽增加![]() 得到一个新矩形
得到一个新矩形![]() ,且矩形
,且矩形![]() 的周长是
的周长是![]() 周长的3倍(如图).同时,矩形
周长的3倍(如图).同时,矩形![]() 的面积和另一个一边长为
的面积和另一个一边长为![]() 的矩形
的矩形![]() 的面积相等,求
的面积相等,求![]() 的值和矩形
的值和矩形![]() 的另一边长.
的另一边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.
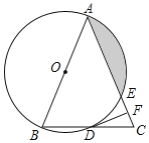
(1)求证:直线DF是⊙O的切线;
(2)求证:BC2=4CFAC;
(3)若⊙O的半径为4,∠CDF=15°,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com