
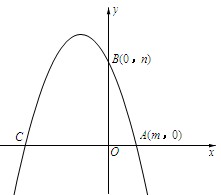
(2011年青海,28,12分已知一元二次方程x2-4x+3=0的两根是m,n且m<n.如图12,若抛物线y=-x2+bx
+c的图像经过点A(m,0)、B(0,n).
(1)求抛物线的解析式.
(2)若(1)中的抛物线与x轴的另一个交点为C.根据图像回答,当x取何值时,抛物线的图像在直线BC的上方?
(3)点P在线段OC上,作PE⊥x轴与抛物线交与点E,若直线BC将△CPE的面积分成相等的两部分,求点P的坐标.
(1)∵x2-4x+3=0的两个根为 x1=1,x2=3
∴A点的坐标为(1,0),B点的坐标为(0,3)
又∵抛物线y=-x2+bx+c的图像经过点A(1,0)、B(0,3)两点
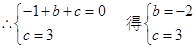
∴抛物线的解析式为 y=-x2-2x+3
(2)作直线BC
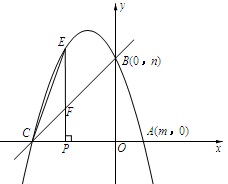
由(1)得,y=-x2-2x+3
∵ 抛物线y=-x2-2x+3与x轴的另一个交点为C 令-x2-2x+3=0
解得:x1=1,x2=-3
∴C点的坐标为(-3,0)
由图可知:当-3<x<0时,抛物线的图像在直线BC的上方.
(3)设直线BC交PE于F,P点坐标为(a,0),则E点坐标为(a,-a2-2a+3)
∵直线BC将△CPE的面积分成相等的两部分.
∴F是线段PE的中点.
即F点的坐标是(a, )
)
∵直线BC过点B(0.3)和C(-3,0)
易得直线BC的解析式为y=x+3
∵点F在直线BC上,所以点F的坐标满足直线BC的解析式
即 =a+3
=a+3
解得 a1=-1,a2=-3(此时P点与点C重合,舍去)
∴P点的坐标是(-1,0)
【解析】略


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源:2011年初中毕业升学考试(青海卷)数学 题型:解答题
(2011年青海,23,7分)学校在艺术周上,要求学生制作一个 精美的轴对称图形,请你用所给出的几何图形:○○△
精美的轴对称图形,请你用所给出的几何图形:○○△ △ (两个圆,两个等边三角形,两条线段)为构件,构思一个独特,有意义的轴对称图形,并写上一句简要的解说词。
△ (两个圆,两个等边三角形,两条线段)为构件,构思一个独特,有意义的轴对称图形,并写上一句简要的解说词。
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广东清远卷)数学 题型:选择题
(2011年青海,15,3分)在 3.14,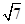 ,π和
,π和 这四个实数中,无理数是( )
这四个实数中,无理数是( )
A. 3.14和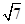 B.π和
B.π和
C. 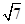 和
和 D.π和
D.π和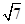
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(四川遂宁卷)数学 题型:解答题
(2011年青海,23,7分)学校在艺术周上,要求学生制作一个精美的轴对称图形,请你用所给出的几何图形:○○△△ (两个圆,两个等边三角形,两条线段)为构件,构思一个独特,有意义的轴对称图形,并写上一句简要的解说词。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com