
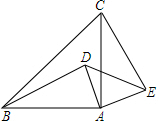
 如图,△ABC与△ADE均是等腰直角三角形,连接BD、CE.
如图,△ABC与△ADE均是等腰直角三角形,连接BD、CE.
分析 (1)根据等腰直角三角形的性质可得AB=AC,AD=AE,∠BAC=∠DAE=90°,于是利用旋转的定义,可把△ABD绕点A顺时针旋转90°得到△ACE,然后根据旋转的性质即可得到BD=CD,BD⊥CD;
(2)分别画出点D、点E旋转后落在△ABC的直角边上的几种特殊情形.
解答 解:(1)BD=CD,BD⊥CD.理由如下:
∵△ABC与△ADE均是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴△ABD绕点A顺时针旋转90°可得到△ACE,
∴BD=CD,BD⊥CD;
(2)
如图1,当点D在AB上,点E在AC上,
∵△ABC与△ADE均是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴BD=CE,BD⊥CE.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.


科目:初中数学 来源: 题型:选择题
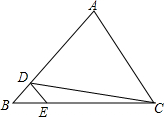 如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )
如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )| A. | 64 | B. | 72 | C. | 80 | D. | 96 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,BC=a,AC=b,AB=c;
在△ABC中,BC=a,AC=b,AB=c;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com