
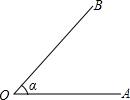
 如图,我们可将这个角表示为
如图,我们可将这个角表示为科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似多边形的性质(带解析) 题型:解答题
八年级数学学习合作小组在学过《图形的相似》这一章后,发现可将相似三角形的定义、判定以及性质拓展到矩形、菱形的相似中去.如:我们可以定义:“长和宽之比相等的矩形是相似矩形.”相似矩形也有以下的性质:相似矩形的对角线之比等于相似比,周长比等于相似比,面积比等于相似比的平方等等.请你参与这个学习小组,一同探索这类问题:
(1)写出判定菱形相似的一种判定方法:若有一组角对应相等(或两组对角线对应成比例),则这两个菱形相似;
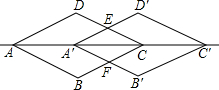
(2)如图,将菱形ABCD沿着直线AC向右平移后得到菱形A′B′C′D′,试证明:四边形A′FCE是菱形,且菱形ABCD∽菱形A′FCE;
(3)若AC= ,菱形A′FCE的面积是菱形ABCD面积的一半,求平移的距离AA′的长.
,菱形A′FCE的面积是菱形ABCD面积的一半,求平移的距离AA′的长.
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似多边形的性质(解析版) 题型:解答题
八年级数学学习合作小组在学过《图形的相似》这一章后,发现可将相似三角形的定义、判定以及性质拓展到矩形、菱形的相似中去.如:我们可以定义:“长和宽之比相等的矩形是相似矩形.”相似矩形也有以下的性质:相似矩形的对角线之比等于相似比,周长比等于相似比,面积比等于相似比的平方等等.请你参与这个学习小组,一同探索这类问题:

(1)写出判定菱形相似的一种判定方法:若有一组角对应相等(或两组对角线对应成比例),则这两个菱形相似;
(2)如图,将菱形ABCD沿着直线AC向右平移后得到菱形A′B′C′D′,试证明:四边形A′FCE是菱形,且菱形ABCD∽菱形A′FCE;
(3)若AC=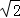 ,菱形A′FCE的面积是菱形ABCD面积的一半,求平移的距离AA′的长.
,菱形A′FCE的面积是菱形ABCD面积的一半,求平移的距离AA′的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com