
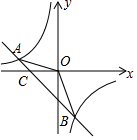
 已知A(-4,2)、B(n,-4)两点是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$图象的两个交点.
已知A(-4,2)、B(n,-4)两点是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$图象的两个交点.分析 (1)先把点A的坐标代入反比例函数解析式,即可得到m=-8,再把点B的坐标代入反比例函数解析式,即可求出n=2,然后利用待定系数法确定一次函数的解析式;
(2)先求出直线y=-x-2与x轴交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算;
(3)观察函数图象得到当x<-4或0<x<2时,一次函数的图象在反比例函数图象上方,据此可得不等式的解集.
解答  解:(1)把A(-4,2)代入y=$\frac{m}{x}$,得m=2×(-4)=-8,
解:(1)把A(-4,2)代入y=$\frac{m}{x}$,得m=2×(-4)=-8,
所以反比例函数解析式为y=-$\frac{8}{x}$,
把B(n,-4)代入y=-$\frac{8}{x}$,得-4n=-8,
解得n=2,
把A(-4,2)和B(2,-4)代入y=kx+b,得
$\left\{\begin{array}{l}{-4k+b=2}\\{2k+b=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-2}\end{array}\right.$,
所以一次函数的解析式为y=-x-2;
(2)y=-x-2中,令y=0,则x=-2,
即直线y=-x-2与x轴交于点C(-2,0),
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×4=6;
(3)由图可得,不等式kx+b-$\frac{m}{x}$>0的解集为:x<-4或0<x<2.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.解决问题的关键是掌握用待定系数法确定一次函数的解析式.


科目:初中数学 来源: 题型:填空题
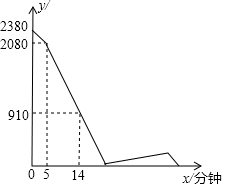 A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是180米.
A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是180米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |$\sqrt{2}-1$|=$\sqrt{2}-1$ | B. | x3•x2=x6 | C. | x2+x2=x4 | D. | (3x2)2=6x4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对某地区现有的16名百岁以上老人睡眠时间的调查 | |
| B. | 对“神舟十一号”运载火箭发射前零部件质量情况的调查 | |
| C. | 对某校九年级三班学生视力情况的调查 | |
| D. | 对某市场上某一品牌电脑使用寿命的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k<2,m>0 | B. | k<2,m<0 | C. | k>2,m>0 | D. | k<0,m<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com