
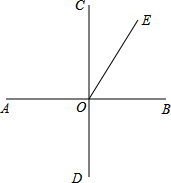
 如图,AB垂直CD(即∠AOC=∠AOD=∠BOD=∠BOC=90°)
如图,AB垂直CD(即∠AOC=∠AOD=∠BOD=∠BOC=90°) 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
 交⊙O于F,GF切⊙O于F且与CP交于G,CH切⊙O于C且与AB的延长线交于H,如果GP2=GD•GC,AD平分∠BAP并交HP于M.
交⊙O于F,GF切⊙O于F且与CP交于G,CH切⊙O于C且与AB的延长线交于H,如果GP2=GD•GC,AD平分∠BAP并交HP于M.| AH |
| AB |
| AE |
| AF |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:AB和CD是两堵和地面BC垂直的墙,两堵墙之间的距离是14米,一个10米长的梯子下端支在地面上某点,上端靠在墙上.
如图:AB和CD是两堵和地面BC垂直的墙,两堵墙之间的距离是14米,一个10米长的梯子下端支在地面上某点,上端靠在墙上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB垂直CD(即∠AOC=∠AOD=∠BOD=∠BOC=90°)
如图,AB垂直CD(即∠AOC=∠AOD=∠BOD=∠BOC=90°)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com