
 (1)如图1,经过平移,△ABC的顶点A移到了点D,请作出平移后的三角形.
(1)如图1,经过平移,△ABC的顶点A移到了点D,请作出平移后的三角形.分析 (1)过C作CF∥AD,CF=CD,过B作BE∥AD,BE=AD,然后再连接DE、FE、DF即可;
(2)首先确定BC的中点D,再连接AD;过B作BE⊥AC,过C作CF平分角ACB,交AB于F.
解答 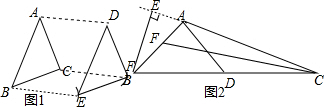 解:(1)如图所示:
解:(1)如图所示:
△DEF即为所求;
(2)如图所示:
BE、AD、CF即为所求.
点评 此题主要考查了作图-平移变换,以及三角形的高、中线、角平分线,关键是掌握从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高.
三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.三角形一边的中点与此边所对顶点的连线叫做三角形的中线.


科目:初中数学 来源: 题型:解答题
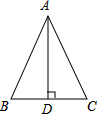 如图,一个以BC为底边的等腰△ABC,底边上的高AD=BC
如图,一个以BC为底边的等腰△ABC,底边上的高AD=BC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
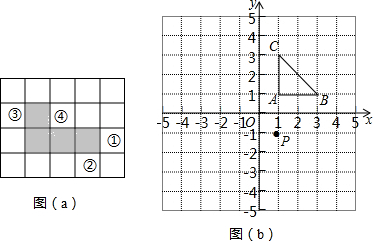
 如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:y=x2-2mx+m2-2与直线x=-2交于点P.
如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:y=x2-2mx+m2-2与直线x=-2交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周体育锻炼的时间 | |
| B. | 某中学调查全校753名学生的身高 | |
| C. | 某学校招聘教师,对应聘人员面试 | |
| D. | 鞋厂检查生产的鞋底能承受的弯折次数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com