
【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

科目:初中数学 来源: 题型:
【题目】把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中,将它绕点C顺时针旋转a角,旋转后的矩形记为矩形EDCF.在旋转过程中,
(1)如图①,当点E在射线CB上时,E点坐标为;
(2)当△CBD是等边三角形时,旋转角a的度数是(a为锐角时);
(3)如图②,设EF与BC交于点G,当EG=CG时,求点G的坐标;
(4)如图③,当旋转角a=90°时,请判断矩形EDCF的对称中心H是否在以C为顶点,且经过点A的抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
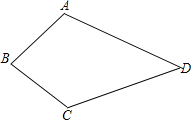
【题目】(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
(B类)已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E. 
(1)求证:MD=ME;
(2)填空:连接OE,OD,当∠A的度数为时,四边形ODME是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2 , 若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解决问题:
(1)如图(1),等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5欲求∠APB的度数,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
请将下列解题过程补充完整。
∵△ACP′≌△ABP,
∴AP′= =3,CP′= =4,∠ =∠APB.
由题意知旋转角∠PA P′=60°,∴△AP P′为 三角形,
P P′=AP=3,∠A P′P=60°。
易证△P P′C为直角三角形,且∠P P′C=90°,
∴∠APB=∠AP′C=∠A P′P+∠P P′C= °+ °= °.
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图(2),△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,
求证:EF2=BE2+FC2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com