
 如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.
如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.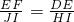 吗?
吗?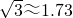 ,结果精确到0.1cm2)?
,结果精确到0.1cm2)?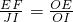 ,
, ,
,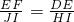 .
.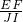 =
=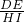 ,
, ,OH=
,OH= +x,∵OI2=OH2+HI2,
+x,∵OI2=OH2+HI2,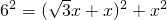 ,
,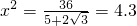 ,
, ),推出即可;
),推出即可; ,OH=
,OH= +x,根据勾股定理得出OI2=OH2+HI2,代入求出即可.
+x,根据勾股定理得出OI2=OH2+HI2,代入求出即可.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.
(2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.| EF |
| JI |
| DE |
| HI |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
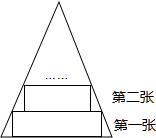 一张等腰三角形纸片,底边长13cm,底边上的高长为32.5cm.现沿底边依次从下往上裁剪宽度均为5cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
一张等腰三角形纸片,底边长13cm,底边上的高长为32.5cm.现沿底边依次从下往上裁剪宽度均为5cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )| A、第3张 | B、第4张 | C、第5张 | D、第6张 |
查看答案和解析>>
科目:初中数学 来源:2011年浙江省台州市中考八校第一次联考数学试卷(解析版) 题型:解答题
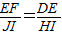 吗?
吗?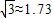 ,结果精确到0.1cm2)?
,结果精确到0.1cm2)?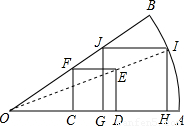
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com