
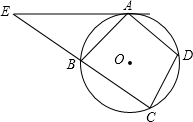
 变,问具备什么条件使原结论成立?(要求画出示意图,注明条件,不要求证明)
变,问具备什么条件使原结论成立?(要求画出示意图,注明条件,不要求证明)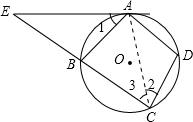 (1)证明:连接AC
(1)证明:连接AC 的中点,
的中点,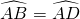 .
.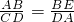
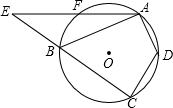
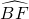 =
=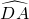 (BF=DA,或∠BCF=∠DCA,或∠BAF=∠DCA,或FA∥BD等),使原结论成立
(BF=DA,或∠BCF=∠DCA,或∠BAF=∠DCA,或FA∥BD等),使原结论成立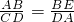 ?AB•DA=CD•BE;
?AB•DA=CD•BE;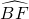 =
=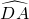 .当
.当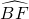 =
=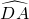 时有∠EAB=∠ACD,而由圆内接四边形的性质知∠ABE=∠ADC,故有△ABE∽△CDA,得
时有∠EAB=∠ACD,而由圆内接四边形的性质知∠ABE=∠ADC,故有△ABE∽△CDA,得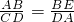 ?AB•DA=CD•BE
?AB•DA=CD•BE

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com