
(本题满分12分)科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程:①在科研所到宿舍楼之间修一条笔直的道路;②对宿舍楼进行防辐射处理,已知防辐射费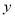 万元与科研所到宿舍楼的距离
万元与科研所到宿舍楼的距离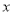
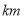 之间的关系式为:
之间的关系式为: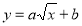 (0≤
(0≤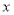 ≤9),当科研所到宿舍楼的距离为1
≤9),当科研所到宿舍楼的距离为1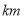 时,防辐射费用为720万元;当科研所到宿舍楼的距离为9
时,防辐射费用为720万元;当科研所到宿舍楼的距离为9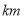 或大于9
或大于9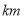 时,辐射影响忽略不计,不进行防辐射处理,设每公里修路的费用为
时,辐射影响忽略不计,不进行防辐射处理,设每公里修路的费用为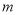 万元,配套工程费
万元,配套工程费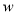 =防辐射费+修路费
=防辐射费+修路费
(1)当科研所到宿舍楼的距离为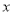 =9
=9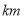 时,防辐射费
时,防辐射费 = 万元;
= 万元;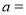 ,
,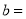
(2)若每公里修路的费用为90万元,求当科研所到宿舍楼的距离为多少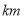 时,配套工程费最少?
时,配套工程费最少?
(3)如果配套工程费不超过675万元,且科研所到宿舍楼的距离小于9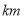 ,求每公里修路费用
,求每公里修路费用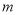 万元的最大值
万元的最大值
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源:2015年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:填空题
如图,在平面直角坐标系中,点P的坐标为(0,4),直线 与
与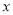 轴、
轴、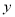 轴分别交于A、B,点M是直线AB上的一个动点,则PM长的最小值为 .
轴分别交于A、B,点M是直线AB上的一个动点,则PM长的最小值为 .

查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(山东济南卷)数学(解析版) 题型:解答题
(9分)抛物线y=ax2+bx+4(a≠0)过点A(1,﹣1),B(5,﹣1),与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图1,连接CB,以CB为边作CBPQ,若点P在直线BC上方的抛物线上,Q为坐标平面内的一点,且CBPQ的面积为30,求点P的坐标;
(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为 上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.
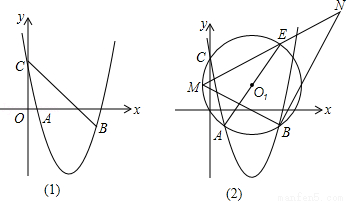
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(山东济南卷)数学(解析版) 题型:选择题
如图,一次函数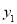 =x+b与一次函数
=x+b与一次函数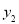 =kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
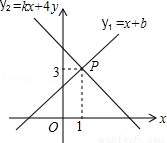
A.x>﹣2 B.x>0 C.x>1 D.x<1
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(山东济南卷)数学(解析版) 题型:选择题
下列运算不正确的是( )
A.a2•a=a3 B.(a3)2=a6 C.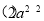 =4a4 D.a2÷a2=a
=4a4 D.a2÷a2=a
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(江苏扬州卷)数学(解析版) 题型:填空题
(本题满分8分)“2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”。小明和小刚参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组
(1)小明被分配到“迷你马拉松”项目组的概率为
(2)求小明和小刚被分配到不同项目组的概率
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(江苏扬州卷)数学(解析版) 题型:填空题
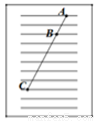
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上,若线段AB=4 cm,则线段BC= cm
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:解答题
阅读材料:用配方法求最值.
已知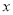 ,
,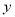 为非负实数,
为非负实数,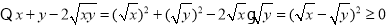 ,
,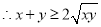 ,当且仅当“
,当且仅当“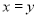 ”时,等号成立.
”时,等号成立.
示例:当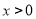 时,求
时,求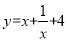 的最小值.
的最小值.
【解析】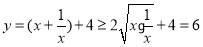 ,当
,当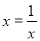 ,即
,即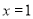 时,
时,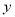 的最小值为6.
的最小值为6.
(1)尝试:当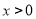 时,求
时,求 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,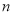 年的保养、维护费用总和为
年的保养、维护费用总和为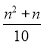 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用= )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com