
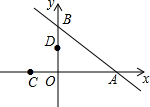
 如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$). 分析 首先连接AD、CD,分别求出点A的坐标、点B的坐标,以及AB的长度是多少;然后根据翻折变换的性质,可得CD=BD,AC=AB=5;最后设点D的坐标为(0,b),在Rt△COD中,根据勾股定理,求出b的值,即可求出点D的坐标.
解答 解:如图1,连接AD、CD,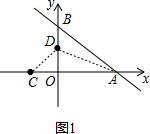 ,
,
∵直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,
∴点A的坐标是(4,0),点B的坐标是(0,3),
∴0A=4,0B=3,
∴AB=$\sqrt{{OA}^{2}{+OB}^{2}}=\sqrt{{4}^{2}{+3}^{2}}=5$,
∵△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,
∴CD=BD,AC=AB=5,
设点D的坐标为(0,b),
则OD=b,BD=3-b,OC=AC-OA=5-4=1,
在Rt△COD中,
∵OD2+OC2=CD2,
∴b2+12=(3-b)2,
解得b=$\frac{4}{3}$,
∴点D的坐标为(0,$\frac{4}{3}$).
故答案为:0,$\frac{4}{3}$.
点评 (1)此题主要考查了翻折变换(折叠问题),要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
(2)此题还考查了一次函数图象上点的坐标特征,要熟练掌握,解答此题的关键是要明确:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
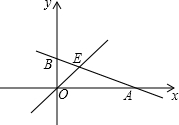 如图,已知函数y=-$\frac{1}{3}x+b$的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
如图,已知函数y=-$\frac{1}{3}x+b$的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
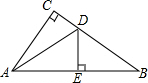 如图,在△ABC中,∠C=90°,点E是斜边AB的中点,ED⊥AB,且∠CAD:∠BAD=5:2,则∠BAC=( )
如图,在△ABC中,∠C=90°,点E是斜边AB的中点,ED⊥AB,且∠CAD:∠BAD=5:2,则∠BAC=( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,A,B,C三点的坐标分别是A(-4,0),B(-$\sqrt{2}$,0),C(1,3).
如图所示,A,B,C三点的坐标分别是A(-4,0),B(-$\sqrt{2}$,0),C(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
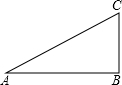 利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.
利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.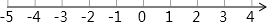
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
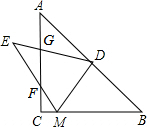 如图,已知点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.若△FCM的周长为16,则斜边AB的长为( )
如图,已知点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.若△FCM的周长为16,则斜边AB的长为( )| A. | 4$\sqrt{2}$ | B. | 8$\sqrt{2}$ | C. | 16$\sqrt{2}$ | D. | 32$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
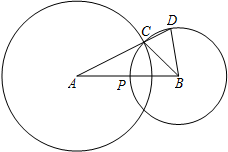 已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.
已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com