
 如图所示,在直线上一点O引一条射线OC,其中OB平分∠AOC,OD平分∠COE,说明BO与DO的关系?
如图所示,在直线上一点O引一条射线OC,其中OB平分∠AOC,OD平分∠COE,说明BO与DO的关系?  培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:022
已知矩形ABCD的长AB=4,宽AD=3,按如图所示放置在直线AP上,然后不滑动地转动,当它转动一周时 ,顶点A所经过的路线长等于________.
,顶点A所经过的路线长等于________.
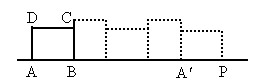
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:068
已知矩形ABCD的长AB=4,宽AD=3,按如图所示放置在直线AP上,然后不滑动地转动,当它转动一周时 ,顶点A所经过的路线长等于________.
,顶点A所经过的路线长等于________.
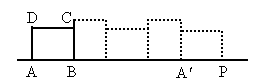
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com