
��7�֣�ͼ�٣�ͼ�ڣ�ͼ�۶���4��4������������ÿ��С�����εĶ����Ϊ��㣬ÿ��С�����εı߳���Ϊ1����ͼ�٣�ͼ�����ѻ����߶�AB����ͼ�����ѻ�����A��������Ҫ��ͼ��

��1����ͼ���У��Ը��Ϊ���㣬ABΪһ��һ�����������Σ�
��2����ͼ���У��Ը��Ϊ���㣬ABΪһ��һ�������Σ�
��3����ͼ���У��Ե�AΪһ�����㣬������������Ҳ�ڸ���ϣ���һ��������������Σ�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015����б�ҵ��ѧ���ԣ����ݱϽھ�����ѧ�������棩 ���ͣ������
����x�ķ���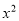 ��4x+3=0��
��4x+3=0��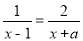 ��һ������ͬ����a= ��
��һ������ͬ����a= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015����б�ҵ��ѧ���ԣ����ɹŰ�����������ѧ�������棩 ���ͣ������
��8�֣���ͼ���ı���ABCDΪ�����Σ���A������Ϊ��0��1������B������Ϊ��0����2��������������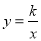 ��ͼ����C��һ�κ���
��ͼ����C��һ�κ���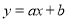 ��ͼ��A��C���㣮
��ͼ��A��C���㣮
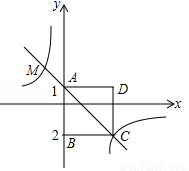
��1������������һ�κ����Ľ���ʽ��
��2������������һ�κ�������һ������M�����ꣻ
��3������P�Ƿ���������ͼ���ϵ�һ�㣬��OAP�����ǡ�õ���������ABCD���������P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015����б�ҵ��ѧ���ԣ����ɹŰ�����������ѧ�������棩 ���ͣ�ѡ����
��3�֣���ͼ��ʾ�ļ����������ͼ�ǣ� ��
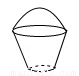
A��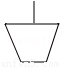 B��
B��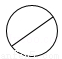 C��
C��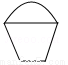 D��
D��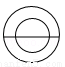
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015����б�ҵ��ѧ���ԣ����־�����ѧ�������棩 ���ͣ������
��8�֣���ͼ�٣��뾶ΪR��Բ�Ľ�Ϊn������������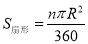 ���ɻ���l=
���ɻ���l=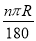 ����
����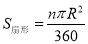 =
=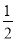 •
•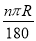 •R=
•R=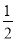 lR��ͨ���۲죬���Ƿ���S����=
lR��ͨ���۲죬���Ƿ���S����=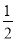 lR������S������=
lR������S������=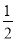 ���ס��ߣ�
���ס��ߣ�
������Σ�����̽���Ȼ�����ͼ�ڣ�����ͬ��ԲΧ�ɵ�Բ�������νصõ�һ���ֽ����Ȼ����������ʽ����Ӧ�ã�
��1�����Ȼ������ΪS�Ȼ���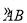 �ij�Ϊ
�ij�Ϊ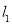 ��
��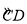 �ij�Ϊ
�ij�Ϊ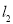 ���߶�AD�ij�Ϊh��������ͬ��Բ�뾶R��r�IJ�����S����=
���߶�AD�ij�Ϊh��������ͬ��Բ�뾶R��r�IJ�����S����=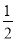 �����ϵ�+�µף����ߣ��ú�
�����ϵ�+�µף����ߣ��ú�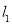 ��
��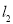 ��h�Ĵ���ʽ��ʾS�Ȼ�����֤����
��h�Ĵ���ʽ��ʾS�Ȼ�����֤����
��2����һ�γ�Ϊ40m�����Χ��һ����ͼ����ʾ���Ȼ��λ����߶�AD�ij�hΪ����ʱ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015����б�ҵ��ѧ���ԣ����־�����ѧ�������棩 ���ͣ������
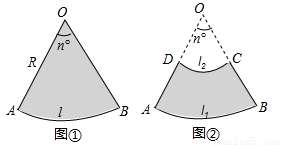
��3�֣���ͼ����Rt��ABC�У���ACB=90�㣬AC=5cm��BC=12cm������ABC�Ƶ�B˳ʱ����ת60�㣬�õ���BDE������DC��AB�ڵ�F�����ACF���BDF���ܳ�֮��Ϊ cm��
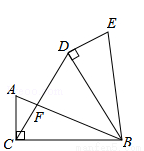
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015����б�ҵ��ѧ���ԣ����������ݾ�����ѧ�������棩 ���ͣ�ѡ����
��ͼ������������ABC�У�AB=AC��BDƽ�֡�ABC����A=36�㣬���1�Ķ���Ϊ�� ��
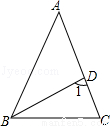
A��36�� B��60�� C��72�� D��108��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015����б�ҵ��ѧ���ԣ����������������ѧ�������棩 ���ͣ�ѡ����
��3�֣�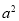 ������ƽ����һ���ǣ� ��
������ƽ����һ���ǣ� ��
A��a B��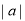 C��
C��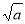 D����a
D����a
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com