
如图,在平面直角坐标系中,⊙M与x轴交于A、B两点,AC是⊙M的直径,过点C的直线交x轴于点D,连接BC,已知点M的坐标为(0, ),直线CD的函数解析式为y=-
),直线CD的函数解析式为y=- x+5
x+5 .
.

(1)求点D的坐标和BC的长;
(2)求点C的坐标和⊙M的半径;
(3)求证:CD是⊙M的切线.
(1)D(5,0);2 .(2)2
.(2)2 ; (3)证明见解析.
; (3)证明见解析.
【解析】
试题分析:(1)因为点M的坐标为(0, ),直线CD的函数解析式为y=-
),直线CD的函数解析式为y=- x+5
x+5 ,D在x轴上,可求出OM=
,D在x轴上,可求出OM= ,D(5,0),又因过圆心M的直径⊥AB,AC是直径,利用垂径定理可得OA=OB,AM=MC,∠ABC=90°,利用三角形的中位线可得OM=
,D(5,0),又因过圆心M的直径⊥AB,AC是直径,利用垂径定理可得OA=OB,AM=MC,∠ABC=90°,利用三角形的中位线可得OM=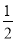 BC,BC=2
BC,BC=2 ;
;
(2)因为BC=2 ,所以可设C(x,2
,所以可设C(x,2 ),利用直线CD的函数解析式为y=-
),利用直线CD的函数解析式为y=- x+5
x+5 .可得到y=-
.可得到y=- x+5
x+5 =2
=2 ,即求出C(3,2
,即求出C(3,2 ),利用勾股定理可得AC=
),利用勾股定理可得AC=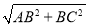 =4
=4 ,即⊙M的半径为2
,即⊙M的半径为2 ;
;
(3)求出BD=5-3=2,BC=2 ,CD=
,CD=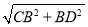 =4,AC=4
=4,AC=4 ,AD=8,CD=4,
,AD=8,CD=4,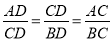 ,可得△ACD∽△CBD,所以∠CBD=∠ACD=90°,CD是⊙M的切线.
,可得△ACD∽△CBD,所以∠CBD=∠ACD=90°,CD是⊙M的切线.
试题解析:(1)【解析】
∵点M的坐标为(0, ),直线CD的函数解析式为y=-
),直线CD的函数解析式为y=- x+5
x+5 ,D在x轴上,
,D在x轴上,
∴OM= ,D(5,0);
,D(5,0);
∵过圆心M的直径⊥AB,AC是直径,
∴OA=OB,AM=MC,∠ABC=90°,
∴OM= BC,
BC,
∴BC=2 .
.
(2)【解析】
∵BC=2 ,
,
∴设C(x,2 );
);
∵直线CD的函数解析式为y=- x+5
x+5 ,
,
∴y=- x+5
x+5 =2
=2 ,
,
∴x=3,即C(3,2 ),
),
∵CB⊥x轴,OB=3,
∴AO=3,AB=6,AC=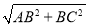 =4
=4 ,
,
即⊙M的半径为2 .
.
(3)证明:∵BD=5-3=2,BC=2 ,CD=
,CD=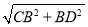 =4,
=4,
AC=4 ,AD=8,CD=4,
,AD=8,CD=4,
∴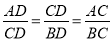 ,
,
∴△ACD∽△CBD,
∴∠CBD=∠ACD=90°;
∵AC是直径,
∴CD是⊙M的切线.
考点:一次函数综合题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年江苏省七年级上学期期中考试数学试卷(解析版) 题型:选择题
飞机上升了-80米,实际上是 ( )
A.上升80米
B.下降 米
米
C.先上升80米,再下降80米
D.下降80米
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A.∠M=∠N B.AM∥CN C.AM=CN D.AB=CD
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作 交AP于E点.
交AP于E点.

(1)求证:DE为⊙O的切线;
(2)若DE=3,AC=8,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在Rt△ABC中,∠ACB=90°,∠B=50°,点D在边BC上,且BD=2CD,把△ABC绕点D逆时针旋转a度(0<a<180°)后,如果点B恰好落在初始Rt△ABC的边上,则a=

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市九年级上学期第一次单元测试数学试卷(解析版) 题型:解答题
下图是泰州某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1 m,拱桥的跨度为10 m,桥洞与水面的最大距离是5 m,桥洞两侧壁上各有一盏距离水面4 m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如下右图).(10分)
(1)求抛物线的关系式;
(2)求两盏景观灯之间的水平距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com