
分析 根据抛物线的平移规律得到平移后的抛物线解析式.设点A(x1,0),B(x2,0),利用根与系数的关系求得AB的距离,由顶点公式求得点C的纵坐标,利用三角形的面积公式,即能求得k值.
解答 解:抛物线y=4x2向下平移k单位后的解析式为:y=4x2-k.
设点A(x1,0),B(x2,0),
∵根与系数的关系得:
x1+x2=0,x1x2=-$\frac{k}{4}$.
∴AB=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{k}$,
又∵顶点C的纵坐标=-k,
∴S△ABC=$\frac{1}{2}$AB•|k|=4,即$\frac{1}{2}$$\sqrt{k}$•|k|=4,
解得k=4.
点评 本题考查了二次函数图象与几何变换.涉及到了二次函数图象的几何变换,根与系数的关系以及三角形的面积,是一道综合性很好的目题.


科目:初中数学 来源: 题型:解答题
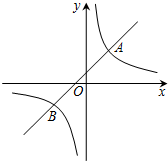 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这一批灯泡是总体 | B. | 每个灯泡是个体 | ||
| C. | 抽取的10个灯泡是样本 | D. | 抽取的10个灯泡的使用寿命是样本 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 旅客上飞机前的安检 | B. | 学校招聘教师,对招聘人员的面试 | ||
| C. | 了解一批灯泡的使用寿命 | D. | 了解701班的身高情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com