在Rt△ABC,∠A=90°,AB=6,AC=8,以斜边BC的中心为旋转中心,把△ABC逆时针方向旋转90°至△DEF,则重叠部分的面积是________.
9
分析:根据S
RQPS=S
△RQC-S
△PSC,依据相似三角形的性质,面积的比等于相似比的平方,即可求解.
解答:

解:根据旋转的性质可知,△PSC∽△RSF∽△RQC,△PSC≌△QFP,
∵∠A=90°,AB=6,AC=8,
∴BC=10,PC=5,S
△ABC=24,
∵S
△PSC:S
△ABC=1:4,即S
△PSC=6,
∴PS=PQ=

,
∴QC=
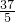
,
∴S
△RQC:S
△ABC=QC
2:BC
2,
S
RQPS=S
△RQC-S
△PSC=9.
故答案为:9.
点评:本题考查旋转的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点-旋转中心;②旋转方向;③旋转角度.

 解:根据旋转的性质可知,△PSC∽△RSF∽△RQC,△PSC≌△QFP,
解:根据旋转的性质可知,△PSC∽△RSF∽△RQC,△PSC≌△QFP, ,
,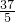 ,
,

 阅读快车系列答案
阅读快车系列答案