
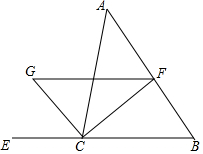
 如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数.
如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数. 分析 首先利用三角形的外角等于不相邻的两个内角的和求得∠ACE的度数,然后根据角的平分线的定义求得∠GCE的度数,再利用平行线的性质求得∠FGC;利用角的平分线的定义可以得到∠FCG=∠ACF+∠ACG=$\frac{1}{2}$(∠ACB+∠ACE),从而求得∠FCG.
解答 解:∵∠ACE=∠A+∠B=45°+55°=100°,
又∵CG是∠ACE的平分线,
∴∠GCE=∠ACG=$\frac{1}{2}$∠ACE=50°,
∵FG∥BC,
∴∠FGC=∠GCE=50°.
∵CF平分∠ACB,
∴∠ACF=$\frac{1}{2}$∠ACB,
又∵∠ACG=$\frac{1}{2}$∠ACE,
∴∠FCG=∠ACF+∠ACG=$\frac{1}{2}$∠ACB+$\frac{1}{2}$∠ACE=$\frac{1}{2}$×180°=90°.
点评 本题考查了三角形角的平分线以及三角形的外角的性质,证得∠FCG=$\frac{1}{2}$(∠ACB+∠ACE)是关键.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:选择题
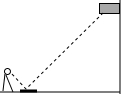 如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )
如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小明的眼睛与地面距离为1.5m,则旗杆的高度为(单位:m)( )| A. | $\frac{16}{3}$ | B. | 9 | C. | 12 | D. | $\frac{64}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
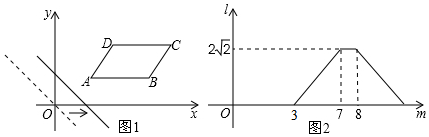
| A. | 10 | B. | 10$\sqrt{5}$ | C. | 5 | D. | 5$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
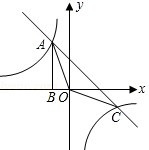 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B且S△ABO=$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com