练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．解方程：
    （1）$\frac{2x+1}{x-1}$=3                           
    （2）$\frac{2x}{x+3}+1=\frac{7}{2x+6}$．

    分析 各分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

    解答 解：（1）去分母得：2x+1=3x-3，
    解得：x=4，
    经检验x=4是分式方程的解；
    （2）去分母得：4x+2x+6=7，
    移项合并得：6x=1，
    解得：x=$\frac{1}{6}$，
    经检验x=$\frac{1}{6}$是分式方程的解．

    点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

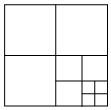    12．如图，将一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪裁成四个小正方形，如此继续下去，…，根据以上操作方法，请你填写表：
    操作次数N12345…n
    正方形的个数47101316…an
    则an=1+3n（用含n的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，∠1=∠FDC，∠2+∠3=180°，证明：AD∥EC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．在一个不透明的口袋中装有2个红球、2个黑球，这些球除颜色外其他都相同，在看不到球的条件下，随机地从这个袋子中摸出一个球，放回后再随机摸出一个球，两次摸到都是红球的概率是（　　）
    A．$\frac{1}{12}$B．$\frac{1}{6}$C．$\frac{1}{4}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．将二次函数y=x2的图象向上平移2个单位后，再向右平移1个单位，所得函数表达式为（　　）
    A．y=（x+1）2+2B．y=（x-1）2+2C．y=（x-1）2-2D．y=（x+1）2-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

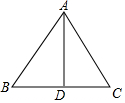    7．如图，已知△ABC中，AB=AC，AD平分∠BAC，请将“等腰三角形三线合一”定理的证明过程补充完整．
    解：∵AD平分∠BAC
    ∴∠BAD=∠CAD（角平分线的定义）
    在△ABD和△ACD中
    AB=AC；
    ∠BAD=∠CAD；
    AD=AD；
    ∴△ABD≌△ACD （SAS）
    ∴BD=DC （全等三角形的对应边相等）
    ∠ADB=∠ADC=$\frac{1}{2}$×180°=90°
    即AD是BC上中线，也是BC上的高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．在平面直角坐标系中，我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”，例如点（-2，-4），（1，2），（3，6）…都是“理想点”，显然这样的“理想点”有无数多个．
    （1）若点M（2，a）是二次函数y=-ax2+ax-2图象上的“理想点”，求这个二次函数的表达式；
    （2）函数y=ax2+ax-1（a为常数，a≠0）的图象上存在“理想点”吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．李明准备进行如下操作实验：把一根长40cm的铁丝剪成两段，并把每段首尾相连各围成一个正方形．李明认为这两个正方形的面积之和不可能等于48cm2．你认为他的说法正确吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某商场设立了一个可以自由转动的转盘，并规定：顾客购物100元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品，下表是活动进行中的一组统计数据：
    转动转盘的次数n　　1001502005008001000
    　落在“玩具车”的次数m　67111143347567702
    　落在“玩具车”的频率　0.670.740.7150.6940.705a
    （1）a=0.702
    （2）我们知道，当n足够大时，频率将会接近一个常数p，则p约为0.7（精确到十分位）．
    （3）假如你去转动转盘一次，你获得玩具车的概率大约是多少？

    查看答案和解析>>

    同步练习册答案