
如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )

A.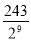 B.
B.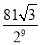 C.
C.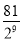 D.
D.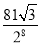
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年江西省七年级上学期期末考试数学试卷(解析版) 题型:选择题
一项工程甲单独做要40天完成,乙单独做要50天完成,甲先单独做4天,然后两人合作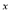 天完成这项工程,则可列的方程是( )
天完成这项工程,则可列的方程是( )
A.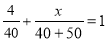 B.
B.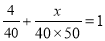
C.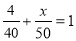 D.
D.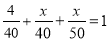
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(山东潍坊卷)数学(解析版) 题型:填空题
观光塔是潍坊市的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.

查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(山东威海卷)数学(解析版) 题型:解答题
如图1,直线y=k1x与反比例函数y=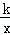 (k≠0)的图象交于点A,B,直线y=k2x与反比例函数y=
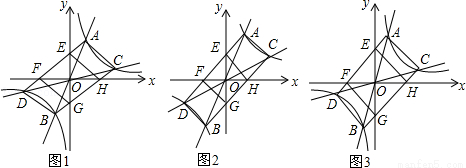
(k≠0)的图象交于点A,B,直线y=k2x与反比例函数y=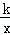 的图象交于点C,D,且k1•k2≠0,k1≠k2,顺次连接A,D,B,C,AD,BC分别交x轴于点F,H,交y轴于点E,G,连接FG,EH.
的图象交于点C,D,且k1•k2≠0,k1≠k2,顺次连接A,D,B,C,AD,BC分别交x轴于点F,H,交y轴于点E,G,连接FG,EH.
(1)四边形ADBC的形状是 ;
(2)如图2,若点A的坐标为(2,4),四边形AEHC是正方形,则k2= ;
(3)如图3,若四边形EFGH为正方形,点A的坐标为(2,6),求点C的坐标;
(4)判断:随着k1、k2取值的变化,四边形ADBC能否为正方形?若能,求点A的坐标;若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(山东威海卷)数学(解析版) 题型:填空题
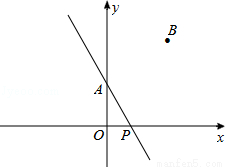
如图,点A、B的坐标分别为(0,2),(3,4),点P为x轴上的一点,若点B关于直线AP的对称点B′恰好落在x轴上,则点P的坐标为 (如图,点A、B的坐标分别为(0,2),(3,4),点P为x轴上的一点,若点B关于直线AP的对称点B′恰好落在x轴上,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(山东威海卷)数学(解析版) 题型:选择题
下列运算正确的是( )
A.(﹣3mn)2=﹣6m2n2
B.4x4+2x4+x4=6x4
C.(xy)2÷(﹣xy)=﹣xy
D.(a﹣b)(﹣a﹣b)=a2﹣b2
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(山东日照卷)数学(解析版) 题型:解答题
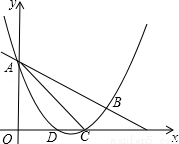
(14分)如图,抛物线y= x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣ x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下:
(1)P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒 个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com