练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

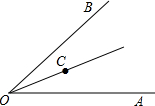
    作业宝如图，∠AOB=60°，OC平分∠AOB，如果射线OA上的点E满足△OCE是等腰三角形，那么∠OEC的度数为________．

    120°或75°或30°
    分析：求出∠AOC，根据等腰得出三种情况，OE=CE，OC=OE，OC=CE，根据等腰三角形性质和三角形内角和定理求出即可．
    解答：
    解：∵∠AOB=60°，OC平分∠AOB，
    ∴∠AOC=30°，
    ①当E在E1时，OE=CE，
    ∵∠AOC=∠OCE=30°，
    ∴∠OEC=180°-30°-30°=120°；
    ②当E在E2点时，OC=OE，
    则∠OCE=∠OEC=（180°-30°）=75°；
    ③当E在E3时，OC=CE，
    则∠OEC=∠AOC=30°；
    故答案为：120°或75°或30°．
    点评：本题考查了角平分线定义，等腰三角形性质，三角形的内角和定理的应用，用了分类讨论思想．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

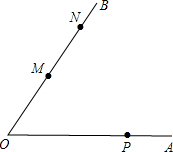    精英家教网如图，∠AOB=60°，M，N是OB上的点，OM=4，MN=2
    		3
    ．
    （1）设⊙O过点M、N，C、D分别是MN同侧的圆上点和圆外点．求证：∠MCN＞∠MDN；
    （2）若P是OA上的动点，求∠MPN的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

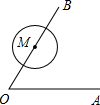    精英家教网如图，∠AOB=60°，点M是射线OB上的点，OM=4，以点M为圆心，2cm为半径作圆．若OA绕点O按逆时针方向旋转，当OA和⊙M相切时，OA旋转的角度是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

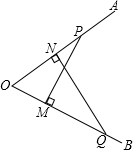    如图，∠AOB=60°，P、Q两点分别由O点沿OA、OB方向同时移动，移动速度分别为a米/秒和b米/精英家教网秒，过P、Q分别作PM⊥OB于M，QN⊥OA于N，求：
    （1）△POM与△QON的周长之比与面积之比；
    （2）若在移动过程中，P与N重合时，求
    ab
    的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•金华模拟）如图，∠AOB=60°，点P在∠AOB的角平分线上，OP=10cm，点E、F是∠AOB两边OA，OB上的动点，当△PEF的周长最小时，点P到EF距离是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，∠AOB=60°，OC是∠AOB的平分线，则∠AOC=
    30
    30
    度．

    查看答案和解析>>

    同步练习册答案