
 解:∵△ABC中,∠BAC=50°,∠ABC=60°,
解:∵△ABC中,∠BAC=50°,∠ABC=60°,| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
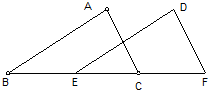 20、如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你在其中选3个作为条件,余下的1个作为结论,使其成为一个真命题,并加以证明.
20、如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你在其中选3个作为条件,余下的1个作为结论,使其成为一个真命题,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有六个条件,请你在其中选三个作为已知条件,余下的选一个作为结论,编写出一个真命题,并说明理由.①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF;⑤∠ACB=∠DEF;⑥∠A=∠D(填写序号即可)
如图所示,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有六个条件,请你在其中选三个作为已知条件,余下的选一个作为结论,编写出一个真命题,并说明理由.①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF;⑤∠ACB=∠DEF;⑥∠A=∠D(填写序号即可)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知BC∥EF,且BC=EF,AF=CD,则AB=DE,说明理由.
如图,已知BC∥EF,且BC=EF,AF=CD,则AB=DE,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com