
阅读以下短文,然后解决下列问题:
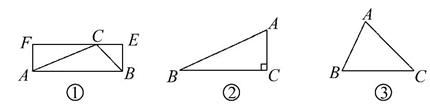
如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”.如图①所示,矩形ABEF即为△ABC的“友好矩形”.显然,当△ABC是钝角三角形时,其“友好矩形”只有一个.
(1)仿照以上叙述,说明什么是一个三角形的“友好平行四边形”.
(2)如图②,若△ABC为直角三角形,且∠C=90°,在图②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小.
(3)若△ABC是锐角三角形,且BC>AC>AB,在图③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证明.
(1)如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角 形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四
形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四 边形”.
边形”.
 (2)此时共有2个“友好矩形”,如图,矩形BCAD,矩形ABEF.
(2)此时共有2个“友好矩形”,如图,矩形BCAD,矩形ABEF.
易知,矩形BCAD,矩形ABEF的面积都等于△ABC面积的2倍,
∴△ABC的“友好矩形”的面积相等.
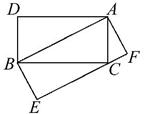
(3)此时共有3个“友好矩形”,如 图中矩形BCDE,矩形CAFG及矩形ABHK,其中矩形ABHK的周长最小.
图中矩形BCDE,矩形CAFG及矩形ABHK,其中矩形ABHK的周长最小.

证明如下:易知,这三个矩形的面积相等,令 其为S.设矩形BCDE,矩形CAFG及矩形ABHK的周长分别为L1,L2,L3,△ABC的边长BC=a,CA=b,AB=c,则L1=
其为S.设矩形BCDE,矩形CAFG及矩形ABHK的周长分别为L1,L2,L3,△ABC的边长BC=a,CA=b,AB=c,则L1=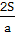 +2a,L2=
+2a,L2=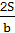 +2b,L3=
+2b,L3=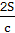 +2c.
+2c.
∴L1-L2=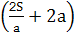 -
-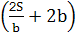 =2(a-b)×
=2(a-b)× ,而ab>S,a>b,∴L1- L2>0,即L1> L2.
,而ab>S,a>b,∴L1- L2>0,即L1> L2.
同理可得,L2> L3,
∴L3最小,即矩形ABHK的周长最小.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
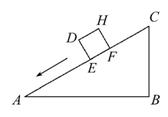
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2m,若∠A=30°,∠B=90°,BC=6m.当正方形DEFH运动到什么位置,即当AE= m时,有DC2=AE2+BC2.
查看答案和解析>>
科目:初中数学 来源: 题型:
声音在空气中传播的速度y( m/s)(简称音速)与气温x(℃)之间的关系
m/s)(简称音速)与气温x(℃)之间的关系 如下:
如下:
| 气温(x/℃) | 0 | 5 | 10 | 15 | 20 |
| 音速 | 331 | 334 | 337 | 340 | 343 |
从表中可知 音速y随温
音速y随温 度x的升高而加快.运动会当天
度x的升高而加快.运动会当天 的气温为20℃,某人看到发令枪的烟0.2s后,听到了枪声,则由此可知,这个人距发令地点 m.
的气温为20℃,某人看到发令枪的烟0.2s后,听到了枪声,则由此可知,这个人距发令地点 m.
查看答案和解析>>
科目:初中数学 来源: 题型:
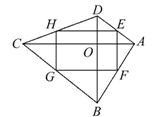
如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB ,BC,CD的中点.若
,BC,CD的中点.若 AC=8,BD=6,则四边形EFGH的面积为 .
AC=8,BD=6,则四边形EFGH的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交 AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )

A.甲 正确,乙错误 B.乙正确,甲错误
正确,乙错误 B.乙正确,甲错误
C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
为响应“节约用水”的号召,小刚随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是( )
A.8,8 B.8.4,8 C.8.4,8.4 D.8,8.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com