
| x-50 |
| 0.5 |
| x-50 |
| 0.5 |


科目:初中数学 来源: 题型:
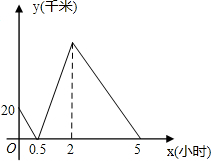 在一条笔直的航道上有A、B、C三个港口,一艘轮船从A港出发,匀速航行到C港后返回到B港,轮船离B港的距离y(千米),与航行时间x(小时)之间的函数关系如图所示,若航行过程中水流速度和轮船的静水速度保持不变,则水流速度为
在一条笔直的航道上有A、B、C三个港口,一艘轮船从A港出发,匀速航行到C港后返回到B港,轮船离B港的距离y(千米),与航行时间x(小时)之间的函数关系如图所示,若航行过程中水流速度和轮船的静水速度保持不变,则水流速度为查看答案和解析>>
科目:初中数学 来源: 题型:
| A、随机掷一枚质地均匀的硬币,正面朝上 |
| B、三角形的内角和等于180° |
| C、买100张中奖率为1%的彩票一定会中奖 |
| D、两个数相加,和大于零 |
查看答案和解析>>
科目:初中数学 来源: 题型:
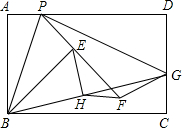 在远古时代,我们的祖先就发现并证明了在直角三角形中斜边上中线等于斜边的一半,今天的我们可以直接运用.现有一张长方形纸片ABCD,在AD边上任取一点P(不与点A、点D重合),以BP所在直线为折痕,将长方形如图翻折,使A点翻到E点,再将PD翻到与PE所在直线位置重合,得到折痕PG,PG与DC边交于点G,点D翻到点F处,如图,连接BG,取BG的中点H,连接HE、HF,试猜想线段HE与HF之间的大小关系,并说明理由.
在远古时代,我们的祖先就发现并证明了在直角三角形中斜边上中线等于斜边的一半,今天的我们可以直接运用.现有一张长方形纸片ABCD,在AD边上任取一点P(不与点A、点D重合),以BP所在直线为折痕,将长方形如图翻折,使A点翻到E点,再将PD翻到与PE所在直线位置重合,得到折痕PG,PG与DC边交于点G,点D翻到点F处,如图,连接BG,取BG的中点H,连接HE、HF,试猜想线段HE与HF之间的大小关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x |
A、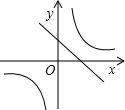 |
B、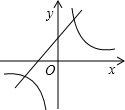 |
C、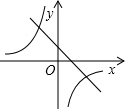 |
D、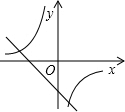 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com