
| 2 | 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| ( 白1,白2) | (白1,白3) | (白1,红) |
| (白2,白1) | (白2,白3) | (白2,红) |
| (白3,白1) | (白3,白2) | (白3,红) |
| (红,白1) | (红,白2) | (红,白3) |
| 6 |
| 12 |
| 1 |
| 2 |
| 3+x+1 |
| 3+x+1+1+x |
| 2 |
| 3 |
| 3+x |
| 3+x+1+x+1 |
| 2 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为8”出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为8”出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
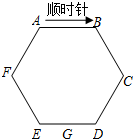 一枚棋子放在边长为1个单位长度的正六边形ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位长度.
一枚棋子放在边长为1个单位长度的正六边形ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com