
 在钓鱼岛海域,我海监船发现一艘非法船只,随即派出快艇拦截,如图为两船航行时路程与时间的函数图象,l1为非法船只航线,l2为我快艇航线,问:
在钓鱼岛海域,我海监船发现一艘非法船只,随即派出快艇拦截,如图为两船航行时路程与时间的函数图象,l1为非法船只航线,l2为我快艇航线,问: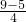 =1海里/分钟,我快艇的速度=
=1海里/分钟,我快艇的速度= =1.5海里/分钟;
=1.5海里/分钟; ,
, x.
x. x,
x,

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
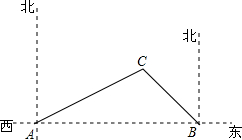 钓鱼岛是我国的固有领土,但却被日本攫为己有.今有我保钓船一艘进入钓鱼岛海域宣示主权.在从钓鱼岛海域返航途中,保钓船不幸在C处抛锚.此时,我国海监船在B处,日本海保厅的巡逻船在我国海监船B的正西方向的A处.现通过卫星定位测得:保钓船在A的北偏东60°方向,在B的北偏西45°方向.此时,日本海保厅立即沿AC方向以500米/分的速度驶向距离10 000米外的保钓船,欲行抓扣.同时我国海监船立即沿BC方向驶向保钓船施救,请问,我国海监船欲赶在日本海保厅的巡逻船之前施救保钓船,其航行速度至少为多少?请说明理由.(适用数据:
钓鱼岛是我国的固有领土,但却被日本攫为己有.今有我保钓船一艘进入钓鱼岛海域宣示主权.在从钓鱼岛海域返航途中,保钓船不幸在C处抛锚.此时,我国海监船在B处,日本海保厅的巡逻船在我国海监船B的正西方向的A处.现通过卫星定位测得:保钓船在A的北偏东60°方向,在B的北偏西45°方向.此时,日本海保厅立即沿AC方向以500米/分的速度驶向距离10 000米外的保钓船,欲行抓扣.同时我国海监船立即沿BC方向驶向保钓船施救,请问,我国海监船欲赶在日本海保厅的巡逻船之前施救保钓船,其航行速度至少为多少?请说明理由.(适用数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•湘西州)钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.
(2013•湘西州)钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.查看答案和解析>>
科目:初中数学 来源: 题型:
 中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.查看答案和解析>>
科目:初中数学 来源: 题型:
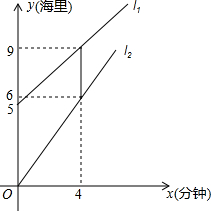 在钓鱼岛海域,我海监船发现一艘非法船只,随即派出快艇拦截,如图为两船航行时路程与时间的函数图象,l1为非法船只航线,l2为我快艇航线,问:
在钓鱼岛海域,我海监船发现一艘非法船只,随即派出快艇拦截,如图为两船航行时路程与时间的函数图象,l1为非法船只航线,l2为我快艇航线,问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com