
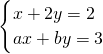 只有正数解,求a,b的所有可能值.
只有正数解,求a,b的所有可能值.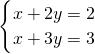 ,解得
,解得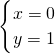 (0,舍去);(2)
(0,舍去);(2)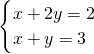 ,解得
,解得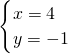 (负值舍去);
(负值舍去);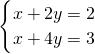 ,解得
,解得 ;(4)
;(4)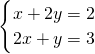 ,解得
,解得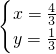 ;
;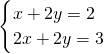 ,解得
,解得 ;(6)
;(6)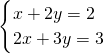 ,解得
,解得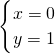 ;
;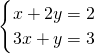 ,解得
,解得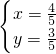 ;(8)
;(8)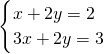 ,解得
,解得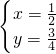 ;
;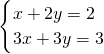 ,解得
,解得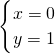 ;(10)
;(10)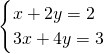 ,解得
,解得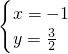 (负值舍去);
(负值舍去);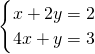 ,解得
,解得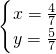 ;(12)
;(12) ,解得
,解得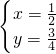 ;
;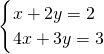 ,解得
,解得 ;(14)
;(14)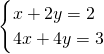 ,解得
,解得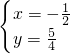 (负值舍去)
(负值舍去)

 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
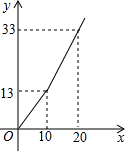 为了鼓励市民节约用水,市政府制定了新的收费标准:设用水量为x吨,需付水费为y元,y与x的函数图象如图.
为了鼓励市民节约用水,市政府制定了新的收费标准:设用水量为x吨,需付水费为y元,y与x的函数图象如图.| A型 | B型 | |
| 成本(万元/套) | 20 | 30 |
| 售价(万元/套) | 25 | 38 |
查看答案和解析>>
科目:初中数学 来源:2009年全国初中数学竞赛(湖南省衡阳市)九年级试卷(解析版) 题型:解答题
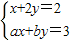 只有正数解,求a,b的所有可能值.
只有正数解,求a,b的所有可能值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com