
已知函数y=![]() x2+6y+10.
x2+6y+10.
(1)当x为何值时,y随x的增大而增大?当x为何值时,y随x的增大而减小?.
(2)当x为何值时,y有最大值或最小值?是多少?.
|
[答案]方法1:配方法. y= 故其图像的对称轴是直线 x=-6,顶点坐标是(-6,-8).(1)∵ (2)∵ 方法 2:公式法∵a= 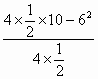 =-8. =-8.
故其图像的对称轴是直线 x=-6,顶点坐标是(-6,-8).(1)∵ (2)∵ [剖析]本题涉及二次函数的增减性,最大(小)值问题,故需先求出其图像的对称轴和顶点坐标,再联系a的符号进行讨论.由于a= |
|
[拓展延伸] (1)对于二次函数y=ax2+bx+c(a≠0)的增减性及最值问题,可用配方法和公式法解决.一般还画出草图,借助图形能更直观地得到答案.(2)对于函数y=ax2+bx+c(a≠0),当a>0时,其图像开口向上,故x<- |


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源:学习周报 数学 北师大九年级版 2009-2010学年 第18期 总第174期 北师大版 题型:044
已知函数y=x2-mx+m-2.
(1)求证:不论m为何实数,此二次函数的图象与x轴都有两个不同的交点;
(2)若函数y有最小值-![]() ,求函数表达式.
,求函数表达式.
查看答案和解析>>
科目:初中数学 来源:2012年浙教版初中数学九年级上2.3二次函数的性质练习卷(解析版) 题型:填空题
已知函数y1=x2与函数y2=- x+3的图象大致如图,若y1<y2,则自变量x的取值范围是 .
x+3的图象大致如图,若y1<y2,则自变量x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
已知函数y=x2-1840 x+1997与x 轴的交点是(m,0)(n,0),则(m2-1841 m+1997)(n2-1841 n+1997)的值是……………………………………………( )
(A)1997 (B)1840 (C)1984 (D)1897
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com