
分析 (1)(2)(5)先算乘方,再利用同底数幂的乘除计算即可;
(3)(6)利用多项式除以单项式的方法计算即可;
(4)先利用平方差公式计算,合并后,再算除法.
解答 解:(1)原式=(9x4y2)÷(-15xy2)•(-9x4y2)
=$\frac{27}{5}$x7y2;
(2)原式=4ab•($\frac{1}{9}$a4b2)÷$\frac{4}{3}$a2b
=$\frac{1}{3}$a3b2;
(3)原式=$\frac{5}{6}$xy3-$\frac{2}{3}$x2y2+1;
(4)原式=[x2y2-4-2x2y2+4]÷(xy)
=[-x2y2]÷(xy)
=-xy;
(5)原式=[a9•(-a12)]÷(a6)÷(a6)
=-a9;
(6)原式=-1.5abc+ab3+0.2.
点评 此题考查整式的混合运算,掌握运算顺序与计算方法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.
如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
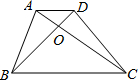 如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少?
如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com