
请阅读下列材料
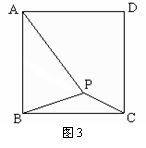
问题:如图1,在等边三角形ABC内有一点P,且PA=2, PB=![]() , PC=1.求∠BPC度数的大小和等边三角形ABC的边长.
, PC=1.求∠BPC度数的大小和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2).连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证).所以∠AP′B=150°,而∠BPC=∠AP′B=150°.进而求出等边△ABC的边长为![]() .问题得到解决.
.问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
 | |||
 |
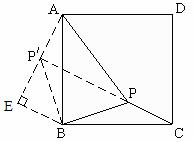
解:(1)如图,将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A.
∴AP′=PC=1,BP=BP′=![]() .
.
连结P P′,
在Rt△BP′P中,
 ∵ BP=BP′=
∵ BP=BP′=![]() ,∠PBP′=90°,
,∠PBP′=90°,
∴ P P′=2,∠BP′P=45°.
在△AP′P中, AP′=1,P P′=2,AP=![]() ,
,
∵ ![]() ,即AP′ 2 + PP′ 2 = AP2.
,即AP′ 2 + PP′ 2 = AP2.
∴ △AP′P是直角三角形,即∠A P′ P=90°.
∴ ∠AP′B=135°.
∴ ∠BPC=∠AP′B=135°.
(2)过点B作BE⊥AP′ 交AP′ 的延长线于点E.
∴ ∠EP′ B=45°.
∴ EP′=BE=1.
∴ AE=2.
∴ 在Rt△ABE中,由勾股定理,得AB=![]() .
.
∴ ∠BPC=135°,正方形边长为![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:阅读理解
| PG |
| PC |
| PG |
| PC |
 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出| PG |
| PC |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 25、请阅读下列材料:
25、请阅读下列材料:查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 25、请阅读下列材料:
25、请阅读下列材料:查看答案和解析>>
科目:初中数学 来源: 题型:
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com