
分析 (1)计算△的值,根据△≥0可得结论;
(2)①先将k=1代入得:y=x2+3x+2,令y=0可以计算抛物线与x轴两个交点坐标,并画出抛物线;
②根据图象找到Q的对称点A的坐标,可得a的取值.
解答 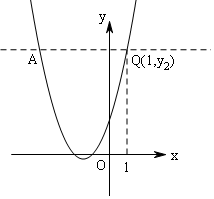 解:(1)kx2+(2k+1)x+2=0,
解:(1)kx2+(2k+1)x+2=0,
△=(2k+1)2-4k×2=4k2+4k+1-8k=4k2-4k+1=(2k-1)2≥0,
∴无论k取任何实数时,关于x的方程kx2+(2k+1)x+2=0总有实数根;
(2)①当k=1时,y=kx2+(2k+1)x+2=x2+3x+2,
当y=0时,x2+3x+2=0,
(x+1)(x+2)=0,
x1=-1,x2=-2,
∴抛物线y=kx2+(2k+1)x+2图象与x轴两个交点坐标分别为(-2,0)、(-1,0),
抛物线如图所示,
②y=x2+3x+2=(x+$\frac{3}{2}$)2-$\frac{1}{4}$,
∴抛物线的对称轴是:x=-$\frac{3}{2}$
由对称性得:点Q关于抛物线对称的对称点A(-4,y2)
∵P(a,y1),Q(1,y2)
∴若y1>y2,实数a的取值范围是a<-4或a>1.
点评 本题考查了一元二次方程根的判别式、二次函数与x轴的交点、顶点式、对称性、画二次函数的图象(五点法),本题虽然用到的知识点较多,但相对比较基础,难度不大,最后一问可以利用数形结合的思想解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
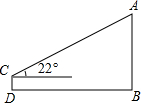 如图,某校数学兴趣小组为了测得学校旗杆的高度AB,在点D处用高为1.2米的测角仪CD,测得旗杆顶端A的仰角为22°,又测得BD=30米,求这根旗杆的高度AB.(精确到0.1米)
如图,某校数学兴趣小组为了测得学校旗杆的高度AB,在点D处用高为1.2米的测角仪CD,测得旗杆顶端A的仰角为22°,又测得BD=30米,求这根旗杆的高度AB.(精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com