
 点A,B在数轴上的位置如图所示,点P是数轴上的一动点.
点A,B在数轴上的位置如图所示,点P是数轴上的一动点.分析 (1)根据PB=3,分两种情况:①点P在点B的左边;②点P在点B的右边;求出点P表示的是什么数即可.
(2)首先分两种情况,求出AP的长度是多少;然后根据点Q是AP的中点,用线段AP的长度除以2,求出线段AQ的长是多少即可.
(3)根据图示,可得当点P在A、B两点之间时,PA+PB的值最小,据此判断即可.
解答 解:(1)①点P在点B的左边时,
∵PB=3,6-3=3,
∴点P表示的是3.
②点P在点B的右边时,
∵PB=3,6+3=9,
∴点P表示的是9.
综上,可得点P表示的是3或9.
(2)∵6-(-2)=8,
∴线段AB的长度是8.
①点P在点B的左边时,
∵AP=8-3=5,5÷2=2.5,
∴线段AQ的长是2.5.
②点P在点B的右边时,
∵AP=8+3=11,11÷2=5.5,
∴线段AQ的长是5.5.
综上,可得
线段AQ的长是2.5或5.5.
(3)根据图示,可得
当点P在A、B两点之间时,PA+PB的值最小,
此时,PA+PB=AB=8,
所以PA+PB的最小值是8.
点评 (1)此题主要考查了两点间的距离,要熟练掌握,解答此题的关键是要明确:连接两点间的线段的长度叫两点间的距离.
(2)此题还考查了数轴的特征和应用,以及分类讨论思想的应用,要熟练掌握.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:填空题
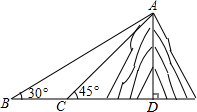 如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为137米(结果保留整数,测角仪忽略不计,$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732)
如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为137米(结果保留整数,测角仪忽略不计,$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
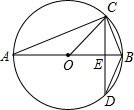 如图,AB是⊙O的直径,CD为弦,CD⊥AB且相交于点E,则下列结论中不成立的是( )
如图,AB是⊙O的直径,CD为弦,CD⊥AB且相交于点E,则下列结论中不成立的是( )| A. | ∠A=∠D | B. | $\widehat{CB}$=$\widehat{BD}$ | C. | ∠ACB=90° | D. | ∠COB=3∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
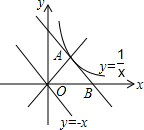 如图,函数y=-x的图象是二、四象限的角平分线,将y=-x的图象以点O为中心旋转90°与函数y=$\frac{1}{x}$的图象交于点A,再将y=-x的图象向右平移至点A,与x轴交于点B,则点B的坐标为(2,0).
如图,函数y=-x的图象是二、四象限的角平分线,将y=-x的图象以点O为中心旋转90°与函数y=$\frac{1}{x}$的图象交于点A,再将y=-x的图象向右平移至点A,与x轴交于点B,则点B的坐标为(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com