
如图,将一副三角板,如图放置在桌面上,让三角板OAB的30°角顶点与三角板OCD的直角顶点重合,边OA与OC重合,固定三角板OCD不动,把三角板OAB绕着顶点O顺时针转动,直到边OB落在桌面上为止。
(1)如下图,当三角板OAB转动了20°时,求∠BOD的度数;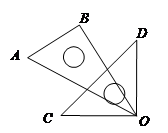
(2)在转动过程中,若∠BOD=20°,在下面两图中分别画出∠AOB的位置,并求出转动了多少度?

(3)在转动过程中,∠AOC与∠BOD有怎样的等量关系,请你给出相等关系式,并说明理由;

(1)40°;(2)转动了40°或80°; (3)∠AOC+∠BOD=60°或∠AOC-∠BOD=60°.
解析试题分析:(1)可直接求出角的度数;(2)要考虑到在∠COD内部和∠COD外部两种情况;(3)要分几种情况加以讨论.
试题解析:(1)∠BOD=90°-∠AOC-∠AOB=90°-20°-30°=40°.(2)如图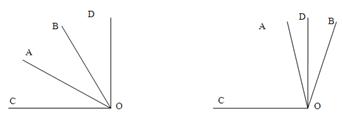
∠AOC=90°-∠BOD-∠AOB ∠AOC= 90°+∠BOD-∠AOB
=90°-20°-30°=40° = 90°+20°-30°=80°
所以转动了40°或转动了80°;
(3)①OB边在∠COD内部或与OD重合,如图:关系式为:∠AOC+∠BOD=60°,理由是
∠AOC+∠BOD=90°-∠AOB=90°-30°=60°;
②OA边在∠COD内部或与OD重合,OB边在∠COD外部,如图:关系式为∠AOC-∠BOD=60°,理由因为∠AOC=90°-∠AOD,∠BOD=30°-∠AOD,
所以∠AOC-∠BOD=(90°-∠AOD)-(30°-∠AOD)=90°-∠AOD-30°+∠AOD=60°;
③OA、OB都在∠COD外部,如图:此时关系式为∠AOC-∠BOD=60°理由为
因为∠AOC=90°+∠AOD,∠BOD=30°+∠AOD,
所以∠AOC-∠BOD=(90°+∠AOD)-(30°+∠AOD)=90°+∠AOD-30°-∠AOD=60°
综合上述:∠AOC与∠BOD的关系为:∠AOC+∠BOD=60°或∠AOC-∠BOD=60°.
考点:角的运算.


科目:初中数学 来源: 题型:解答题
如图,在△ABC中,已知∠ABC=35°,点D在BC上,点E在AC上,∠BAD=∠EBC,AD交BE于F.
(1)求∠BFD的度数;
(2)若EG//AD交BC于G,EH⊥BE交BC于H,求∠HEG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC-CB=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在四边形ABCD中,AD∥BC,点O在AD上,BO、CO分别平分∠ABC、∠DCB,若∠A+∠D=208°,求∠OBC+∠OCB的度数。请你将解答过程补充完整。
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,已知D、E分别是△ABC的AB,AC边上的点,DE∥BC,且S△ADE:S四边形DBCE=1:8,那么AE:AC等于( )
A.1:9 B.1:3 C.1:8 D.1:2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com