
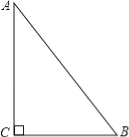
【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.
(1)当t= 时,CP把△ABC的周长分成相等的两部分?
(2)当t= 时,CP把△ABC的面积分成相等的两部分?
(3)当t为何值时,△BCP的面积为12?
【答案】(1)6 (2)6.5 (3)2或6.5
【解析】试题分析:(1)由△ABC的周长为24时,当CP把△ABC的周长分成相等的两部分时,点C所以过的路程为12cm,再求时间即可;(2)由![]() 的面积等于
的面积等于![]() 的一半;设
的一半;设![]() 为
为![]() 的高,则
的高,则![]() ,则
,则![]() ,所以点
,所以点![]() 应为
应为![]() 的中点,所以点运动的路程为
的中点,所以点运动的路程为![]() ,再求时间即可;(3)分两种情况讨论,当点P在AC上时,由
,再求时间即可;(3)分两种情况讨论,当点P在AC上时,由![]() ×6×CP=12,得出CP=4,此时运动时间为2秒;当当P在AB上时,P运动到AB的中点,运动路程为13cm,求时间即可;
×6×CP=12,得出CP=4,此时运动时间为2秒;当当P在AB上时,P运动到AB的中点,运动路程为13cm,求时间即可;
试题解析:
(1)△ABC中,∵AC=8cm,BC=6cm,AB=10cm,∴△ABC的周长=8+6+10=24cm,∴当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,∴2t=12,t=6;(2)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时CA+AP=8+5=13(cm),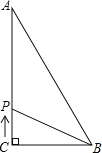
∴2t=13,t=6.5;
(3)分两种情况:①当P在AC上时,∵△BCP的面积=12,即![]() ×6×CP=12,∴CP=4,∴2t=4,t=2;②当P在AB上时,∵△BCP的面积=12=△ABC面积的一半,∴P为AB中点,∴2t=13,t=6.5.故答案为6秒;6.5秒.
×6×CP=12,∴CP=4,∴2t=4,t=2;②当P在AB上时,∵△BCP的面积=12=△ABC面积的一半,∴P为AB中点,∴2t=13,t=6.5.故答案为6秒;6.5秒.


科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
(x-1)(x+1)= ______ ;
(x-1)(x2+x+1)= ______ ;
(x-1)(x3+x2+x+1)= ______ ;
(2)从上面的算式及计算结果,你发现了什么?请根据你发现的规律直接写下面的空格.
(x-1)( ______ )=x6-1;
(3)利用你发现的规律计算:
(x-1)(x6+x5+x4+x3+x2+x+1)= _____ ;
(4)利用该规律计算1+4+42+43+…+42013= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点A、C的坐标分别为(10,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣![]() x+m交线段OA于点E.
x+m交线段OA于点E.
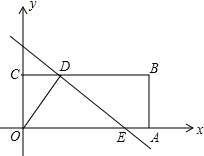
(1)矩形OABC的周长是 ;
(2)连结OD,当OD=DE时,求m的值;
(3)若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC重叠部分的面积是否会随着E点位置的变化而变化,若不变,求出该重叠部分的面积;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题4分+5分=9分)
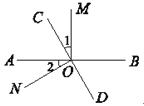
如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOC的度数;(2)若∠1=![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com