
分析 (1)根据“魔幻数组”的定义,找出所有的“魔幻数组”即可得出结论;
(2)根据规律找出n=9,设出这9个数,再根据“科幻数组”的特征找出关于m的一元二次方程,解方程即可得出结论.
解答 解:(1)1,2,3及2,3,4.
(2)由已知可得:
32+42=52,102+112+122=132+142,212+222+232+242=252+262+272,…
故可知n=9,可设这9个数为m-4,m-3,m-2,m-1,m,m+1,m+2,m+3,m+4,则有:
(m-4)2+(m-3)2+(m-2)2+(m-1)2+m2=(m+1)2+(m+2)2+(m+3)2+(m+4)2,
整理得:m2-40m=0,由题意m不为0,故m=40,
∴这9个数为36,37,38,39,40,41,42,43,44.
点评 本题考查了新定义的应用,根据新定义的意义找出方程是解题的关键.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
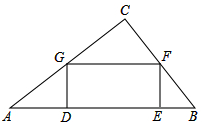 如图,在直角三角形ABC中,∠C=90°,AC=3,BC=4,矩形DEFG内接于△ABC中,如果DG:DE=3:5,求矩形DEFG的周长.
如图,在直角三角形ABC中,∠C=90°,AC=3,BC=4,矩形DEFG内接于△ABC中,如果DG:DE=3:5,求矩形DEFG的周长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com