
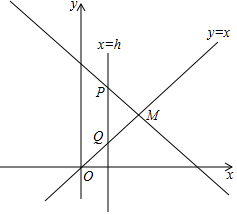
 如图,直线y=x和直线y=-x+5相交于点M,直线PQ⊥x轴,分别交直线y=-x+5和直线y=x于点P、Q,点R是y轴上一点,若△PQR为等腰直角三角形.求点R的坐标.
如图,直线y=x和直线y=-x+5相交于点M,直线PQ⊥x轴,分别交直线y=-x+5和直线y=x于点P、Q,点R是y轴上一点,若△PQR为等腰直角三角形.求点R的坐标. 分析 首先求出PQ的长,分三种情况进行讨论:①如图1,当PR=PQ时,△PQR为等腰直角三角形,根据PQ=PR列方程求得;②如图2,当RQ=PQ时,△PQR为等腰直角三角形,根据PQ=RQ列方程求得;③如图3,当∠PRQ=90°时,△PQR为等腰直角三角形,根据2RB=PQ列方程求得.
解答 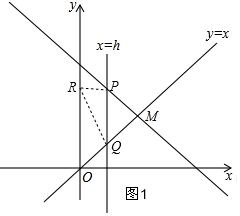 解:设直线PQ的解析式为:x=h,
解:设直线PQ的解析式为:x=h,
∴P(h,-h+5)、Q(h,h),
∴PQ=-h+5-h=5-2h,
分三种情况:
①如图1,过P作PR⊥y轴于R,连接RQ,
当PR=PQ时,△PQR为等腰直角三角形,
∴h=5-2h,
h=$\frac{5}{3}$,
∴-h+5=-$\frac{5}{3}$+5=$\frac{10}{3}$,
∴R(0,$\frac{10}{3}$);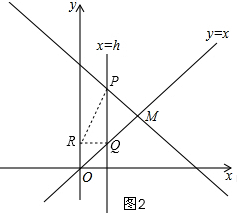
②如图2,过Q作QR⊥y轴于R,连接RP,
当RQ=PQ时,△PQR为等腰直角三角形,
∴h=5-2h,
h=$\frac{5}{3}$,
∴R(0,$\frac{5}{3}$);
③如图3,作线段PQ的中垂线l,交y轴于R,交PQ于B,连接PR、RQ,则PR=RQ,
当∠PRQ=90°时,△PQR为等腰直角三角形,
∴∠PRB=∠QRB=45°,
∴△PBR和△BRQ都是等腰直角三角形,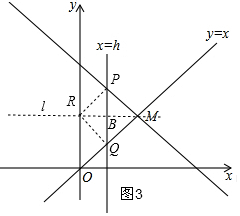
∴2RB=2BQ=PQ,
则2h=5-2h,
h=$\frac{5}{4}$,
∴OR=$\frac{5}{4}$+$\frac{1}{2}$(5-2h)=$\frac{5}{4}$+$\frac{5}{2}$-h=$\frac{5}{2}$,
∴R(0,$\frac{5}{2}$);
综上所述,若△PQR为等腰直角三角形.点R的坐标是(0,$\frac{10}{3}$)或(0,$\frac{5}{3}$)或(0,$\frac{5}{2}$).
点评 本题考查了两直线相交问题以及等腰直角三角形的性质和判定,有难度,根据数形结合的思想进行分类讨论是解本题的关键,等量关系是根据等腰直角三角形的性质列方程求解,注意不要漏解.


科目:初中数学 来源: 题型:解答题
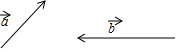 已知两个不平行的向量$\overrightarrow{a},\overrightarrow{b}$,求作向量:2($\overrightarrow{a}-\overrightarrow{b}$)-($\overrightarrow{a}-\frac{3}{2}\overrightarrow{b}$)
已知两个不平行的向量$\overrightarrow{a},\overrightarrow{b}$,求作向量:2($\overrightarrow{a}-\overrightarrow{b}$)-($\overrightarrow{a}-\frac{3}{2}\overrightarrow{b}$)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-1,-2) | C. | (1,2) | D. | (-2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | C、π、R是变量 | B. | C是变量,2、π、R是常量 | ||
| C. | R是变量,2、π、C是常量 | D. | C、R是变量,2、π是常量 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 钉尖着地 | B. | 钉尖不着地 | C. | 一样大 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com