练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．已知平面直角坐标中有一点M（2-a，3a+6），点M到两坐标轴的距离相等，求M的坐标．

    分析 根据点的到两坐标轴距离相等，点M的横坐标与纵坐标相等或互为相反数列方程求出a的值，再求解即可．

    解答 解：∵点M的坐标为（2-a，3a+6），且点M到两坐标轴的距离相等，
    ∴2-a=3a+6或（2-a）+（3a+6）=0，
    解得，a=-1或a=-4，
    ∴M点坐标为（3，3）或（6，-6）．

    点评 本题考查了点的坐标，理解点的到两坐标轴距离相等，点M的横坐标与纵坐标相等或互为相反数两种情况是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．在等边三角形ABC中，E为直线AB上一点，连接EC．ED与直线BC交于点D，ED=EC．
    （1）如图1，AB=1，点E是AB的中点，求BD的长；
    （2）点E是AB边上任意一点（不与AB边的中点和端点重合），依题意，将图2补全，判断AE与BD间的数量关系并证明；
    （3）点E不在线段AB上，请在图3中画出符合条件的一个图形．

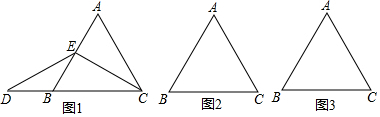
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

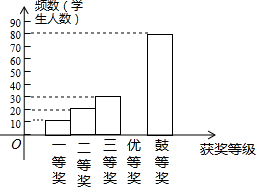    17．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：
    　获奖等次　频数　频率
    　一等奖　10　0.05
    　二等奖　20　0.10
    三等奖　30　b
    　优胜奖　a　0.30
    　鼓励奖　80　0.40
    请根据所给信息，解答下列问题：
    （1）a=60，b=0.15，且补全频数分布直方图；
    （2）若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？
    （3）若我市初中生共有16000人，竞赛活动获奖率为40%，获三等奖以上的学生表示对“足球比较喜欢”，请你估计我市初中生对“足球比较喜欢”的有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

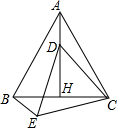    14．如图，等边△ABC中，AH⊥BC于点H，点D是AB上任意一点，以CD为边作等边△CDE，连结BE．
    （1）求证：BE⊥AB；
    （2）当点E在AH的延长线上时，试求$\frac{AD}{AH}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，在矩形ABCD中，AB=8，BC=10，E是AB上一点，将矩形ABCD沿CE折叠后，点B落在AD边的点F上，则AF的长为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．计算$\sqrt{3}$（$\sqrt{27}$-$\sqrt{3}$）的结果是6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．平行四边形ABCD中，AE、BF分别平分∠DAB和∠ABC交CD于点E、F．AE、BF交于点G．
    （1）求证：AE⊥BF；
    （2）判断DE和CF的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

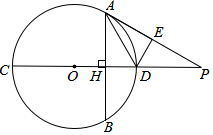    15．如图，CD为⊙O的直径，弦AB垂直于CD，垂足为H，∠EAD=∠HAD．
    （1）求证：AE为⊙O的切线；
    （2）延长AE与CD的延长线交于点P，过D 作DE⊥AP，垂足为E，已知PA=2，PD=1，求⊙O的半径和DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．在等边△ABC中，E是边BC上的一个动点（不与点B，C重合），∠AEF=60°，EF交△ABC外角平分线CD于点F．
    （1）如图1，当点E是BC的中点时，请你补全图形，直接写出$\frac{CF}{AE}$的值，并判断AE与EF的数量关系；
    （2）当点E不是BC的中点时，请你在图（2）中补全图形，判断此时AE与EF的数量关系，并证明你的结论．

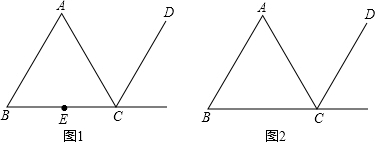
    查看答案和解析>>

    同步练习册答案