
分析 根据分式的运算法则即可求出答案.
解答 解:当a=$\sqrt{3}$-2时,
∴原式=($\frac{1}{a+2}$-$\frac{1}{a-2}$)×$\frac{(a+2)(a-2)}{4(a+2)}$
=($\frac{1}{a+2}$-$\frac{1}{a-2}$)×$\frac{a-2}{4}$
=$\frac{a-2}{4(a+2)}$-$\frac{1}{4}$
=$\frac{a-2}{4(a+2)}$-$\frac{a+2}{4(a+2)}$
=$\frac{-4}{4(a+2)}$
=-$\frac{1}{a+2}$
=-$\frac{1}{\sqrt{3}}$
=-$\frac{\sqrt{3}}{3}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方程$\sqrt{x}$=4的根是x=±16 | |
| B. | 方程$\sqrt{2x+3}$=x的根是x1=3,x2=-1 | |
| C. | 方程$\sqrt{2x-1}$=x+1变形所得的有理方程是2x-1=x2+1 | |
| D. | 方程$\sqrt{x+1}$+1=0没有实数解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解我市中学生每天进行体育锻炼的时间情况,随机抽样调查了200名中学生,根据调查结果得到如图所示的统计图表,请根据图表信息解答下列问题:
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解我市中学生每天进行体育锻炼的时间情况,随机抽样调查了200名中学生,根据调查结果得到如图所示的统计图表,请根据图表信息解答下列问题:| 类别 | 时间t(小时) | 人数 |
| A | t≤0.5 | 10 |
| B | 0.5<t≤1 | 40 |
| C | 1<t≤1.5 | a |
| D | 1.5<t≤2 | 60 |
| E | t>2 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
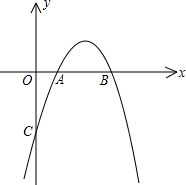 如图.已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4.
如图.已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com