
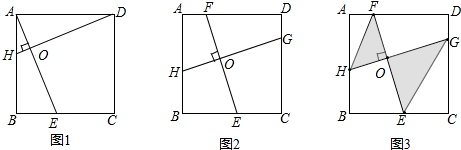
| AF |
| CE |
| FH |
| EG |
| FO |
| OE |
| 1 |
| 2 |
| 17 |
| FO |
| FE |
| HO |
| HG |
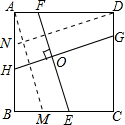
| AF |
| CE |
| FH |
| EG |
| FO |
| OE |
| 1 |
| 2 |
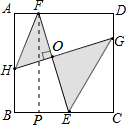 根据勾股定理得EF=
根据勾股定理得EF=| 17 |
| FO |
| FE |
| HO |
| HG |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 17 |
| 18 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 68 |
| 18 |
| 85 |
| 18 |


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
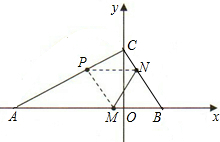 如图,已知A(-3,0),C(0,
如图,已知A(-3,0),C(0,| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
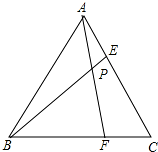 等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:
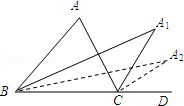 如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空:
如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空:查看答案和解析>>
科目:初中数学 来源: 题型:
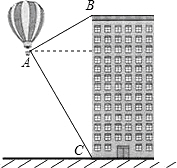 热气球的探测器显示,从热气球底部A处看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球A处与高楼的水平距离为120m,这栋高楼有多高(
热气球的探测器显示,从热气球底部A处看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球A处与高楼的水平距离为120m,这栋高楼有多高(| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com