
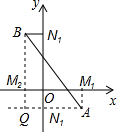
 阅读材料:
阅读材料:| (x2-x1)2+(y2-y1)2 |
| 13 |
| 4 |
| 13 |
| 4 |
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |
| (x2-x1)2+(y2-y1)2 |
| 4 |
| 3 |
| 13 |
| 3 |
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |
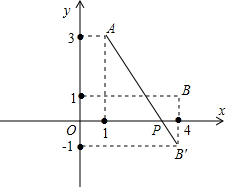 解:(1)|AB|=
解:(1)|AB|=| (-2-1)2+(1+3)2 |
| 4 |
| 3 |
| 13 |
| 3 |
| 13 |
| 4 |
| 13 |
| 4 |
| (4-1)2+(-1-3)2 |
| 13 |
| 4 |
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |
| (x-0)2+(y-2)2 |
| (x-3)2+(y-1)2 |
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |
| (0-3)2+(2-1)2 |
| 10 |


科目:初中数学 来源: 题型:阅读理解
| x |
| x+2 |
| 3 | x |
| 3 | x-1 |
| 3 |
| x |
| 3 |
| x |
| 3 |
| x+2 |
| 3 |
| x-1 |
| 3 |
| x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:2012年广东省汕头市中考数学模拟试卷(解析版) 题型:解答题
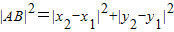 .
.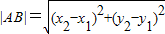 .
.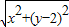 +
+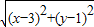 的最小值.
的最小值.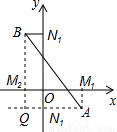
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
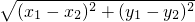 .例如:若
.例如:若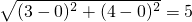 .
.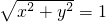 ,即x2+y2=1成立;反过来,如果点P(x,y)的坐标满足等式x2+y2=1,那么点P必在⊙O上,这时,我们就把等式x2+y2=1称为⊙O的方程.
,即x2+y2=1成立;反过来,如果点P(x,y)的坐标满足等式x2+y2=1,那么点P必在⊙O上,这时,我们就把等式x2+y2=1称为⊙O的方程.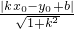 .
. 的距离.
的距离. ,其中n≠0,m>0.
,其中n≠0,m>0.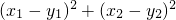 是与n无关的常数,并求出这个常数.
是与n无关的常数,并求出这个常数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com