
 如图点M,N在反比例函数
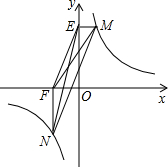
如图点M,N在反比例函数 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.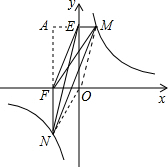 证明:连接MO,NO,延长FN,作EA⊥FN于点A,
证明:连接MO,NO,延长FN,作EA⊥FN于点A, (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴, k,S△EMO=S△EFM=
k,S△EMO=S△EFM= k,
k, (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,连接MO,NO,延长FN,作EA⊥FN于点A,得出△EFM与△EOM等底同高,△EFN与△FNO等底同高,进而得出S△EFM=S△FNO=
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,连接MO,NO,延长FN,作EA⊥FN于点A,得出△EFM与△EOM等底同高,△EFN与△FNO等底同高,进而得出S△EFM=S△FNO= k,S△EMO=S△EFM=
k,S△EMO=S△EFM= k,得出答案即可.
k,得出答案即可.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com