
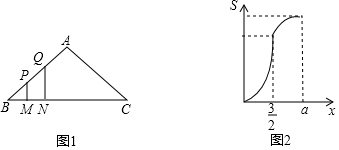
���� ��1����ͼ2��֪BC=$\frac{3}{2}$��4=6����a=6��2=3������PM=QN���ɶԳƵ����ʵõ�����x�ķ��̣��ⷽ�̼�����⣻
��2���������������0��x��$\frac{3}{2}$����$\frac{3}{2}$��x��3���������ۿ���S����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��� �⣺��ͼ2��֪BC=$\frac{3}{2}$��4=6����a=6��2=3��
��1����������
x=6-2x��
���x=2��
��2����0��x��$\frac{3}{2}$��S=2x��2x��2-x2��2=$\frac{3}{2}$x2��
��$\frac{3}{2}$��x��3��S=��x+6-2x����6-x-6+2x����2=-$\frac{1}{2}$x2+3x��
����������S����x�ĺ�����ϵʽ��S=$\frac{3}{2}$x2��0��x��$\frac{3}{2}$����S=-$\frac{1}{2}$x2+3x��$\frac{3}{2}$��x��3����
�ʴ�Ϊ��2��
���� ���⿼���˶�������ĺ���ͼ���漰�����������ε����ʣ��ԳƵ����ʣ������ε�������ı��ε�������Ƚϸ��ӣ�һ���ڽ����������ʱ����ȡ���ν����������۵�˼�룮


 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -1 | C�� | 0 | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ${x^2}+\frac{1}{x^2}$=0 | B�� | ��x-1��x=1 | C�� | ax2+bx=0 | D�� | x2-xy-y2=0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com