
已知抛物线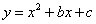 与x轴交于点
与x轴交于点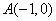 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
(1)求抛物线的解析式;
(2)若抛物线向下平移k个单位后经过点(-5,6)。
①求k的值及平移后抛物线所对应函数的最小值;
②设平移后抛物线与y轴交于点D,顶点为Q,点M是平移后的抛物线上的一个动点。请探究:当点M在何处时,△MBD的而积是△MPQ面积的2倍?求出此时点M的坐标。
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
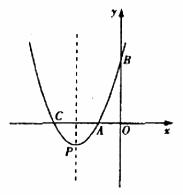
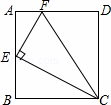
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:
①∠AEF=∠BCE;
②AF+BC>CF;
③S△CEF=S△EAF+S△CBE;
④若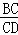 =
= ,则△CEF≌△CDF.
,则△CEF≌△CDF.
其中正确的结论是 .(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
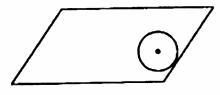
如图,公园里有一块平行四边形的草坪,草坪里有一个圆形花坛,有关部门计划在草坪上修一条小路,这条小路要把草坪和花坛的面积同时平分,请在图中画出这条小路。(小路用AB表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
)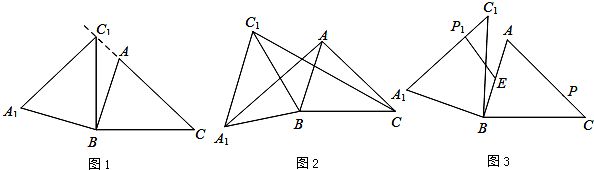 在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P 的对应点是点P1,求线段EP1长度的最大值与最小值.
的对应点是点P1,求线段EP1长度的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com